欢迎
· 阅读需 1 分钟
欢迎来到我的博客！
todo-list
· 阅读需 1 分钟
- 拉插优化 dp
- 树状数组优化 dp
- 树状数组
- 加训数论
- 线段树优化 dp
tips
· 阅读需 1 分钟
因为本人太菜所以放一点可能相关的思考在这里（自己都不一定能记得啥时候回来看
有二元关系时可以尝试连边
字符集小就考虑枚举字符关系
位置关系不重要就先排序
模拟赛题解/2025.10.22 模拟赛
· 阅读需 10 分钟
T1-动态构图（dynamic）
题面
阿狸有一个包含 个节点，初始有 条边的无向联通图 。由于他的朋友都去度假了，没人跟他研究图论算法，所以他决定自己用这个无向图做一个游戏。
游戏分为多个回合。每一回合，阿狸会新建一个与无向图 完全相同的副本 ，然后枚举三个不同的节点 ，如果 均在 上存在边，而 在 上没有连边，则阿狸会在 上建立 这条边。在所有可以添加的边均加入 后，阿狸会让 ，并结束该回合。
在某个回合结束后，若对于任意两个不同的节点 ，都满足 这条边在 中存在，则游戏立即结束，阿狸的最终得分为游戏经过的回合数量。如果初始的 已经满足了该条件，则回合数是 0。
。
题解
先考虑一条链上会发生什么，简单模拟发现内容近似于每个点向旁边的另一个点合并，显然轮次是 （ 是序列长度）。
在图上，轮次取决于最长的一条链，于是问题转化成求最长链长度的 。
注意到，从任何一个点出发，一定存在一个点满足两点之间的距离超过最长链长度的一半。
- 证明：假设有一个点 不满足该性质，则剩余点两两之间的距离都不会超过它们分别与 的距离和，于是发现最长链长度小于最长链长度，矛盾。
所以只需要选择一个点，从该点出发找到距离最远的点，其距离的 一定是最长链的 或少 。
由于可以给出两个点，只要其中之一正确即可，因此可以直接输出 和其 。
T2-重力排序（epotential）
题面
阿狸找到了无限多的、五颜六色的沙块，于是他决定用这些沙块建一个三角形建筑。在此过程中，他注意到沙块是不能悬空，于是他发现了一种新的排序算法：重力排序。
阿狸先选择了一个 的排列 ，以及长度为 的颜色序列 。在选择 之后，他决定实行重力排序算法。
具体而言，重力排序算法是这样实现的：对于所有满足 的 ，在所有 的位置 上放置一个颜色为 的沙块。随后，施加向下的重力，使所有沙块尽可能下落。
这里，位置 表示从上往下第 行、从左往右第 列的格子。
在算法实现后，阿狸给重力排序后的结果拍了照片。
不过阿狸是一个好奇心很强的人。阿狸希望你来计算，有多少个不同的排列 （注意 可以是 本身），使得在用 来完成重力排序算法之后，每个位置上的沙块颜色与照片中的相同。
两个排列 不同，当且仅当存在正整数 ，满足 。
阿狸没时间记忆过大的数字，所以你的答案要对 998244353 取模。
。
题解
观察样例，不难发现对于同色的第 两行，如果它们的 可以相互交换，那么对于任意正整数 ，有 。
很多人可能会想到，直接连边然后算连通块大小的阶乘乘积，但这是错误的，比如 时， 不是一个合法解。
考虑枚举 ，找到 的这个位置 ，然后计算 这一行能出现在 的哪些位置。在不管 对应值 的那些行的情况下， 可以交换到的位置一定是一个连续的段，也就是 所在的极长连续段。链表和并查集维护即可。
T3-魔法对轰（apollyon）
题面
阿狸有一块长 米，宽 1 米的白板。他将这块白板划分为一排的 个格子，每个格子的长宽均为 1 米。他让这些格子从左到右依次编号为 。
阿狸有 种魔法，第 种魔法可以让编号 范围内的格子染上颜色 。如果某个格子被多次染色，以最后一次的颜色为准。
阿狸需要使用每种魔法恰好一次，但可以决定每种魔法的施展顺序。请帮他决定一个顺序，使得最终对于每个正整数 ，第 个格子最终的颜色与 相同。
。
题解
注意到每个位置对应的权值只与覆盖这一位置的最后一次操作有关，所以考虑倒序选择操作。
问题变为，如果某个位置被操作一次，则颜色被永久保留，求一组方案。那么，在一个位置被涂色后，可以任意对其做其余操作。
考虑贪心策略。每次选一个当前可以选择区间，标记这个区间内的所有位置。如果对于某个区间包含的每个位置，要么被标记，要么其颜色与操作对应相同，则这个区间就是可以选择的。
容易得出，这样选择一定不劣，复杂度为 。
上述做法显然不能通过，需要优化。这里用到了一个 trick。
使用线段树，将每个操作区间拆成 级别个线段树上的不交子区间，如果这些区间是可以被选择的，那么整个原来的区间也是可以被选择的。
维护每个位置对应的需要涂的颜色，记录线段树每个节点的 ：
- 如果这个线段树节点对应区间中，每个位置均被标记，即整个区间剩下的涂色方案可以任意，则 为 0。
- 如果这个区间中，除了被标记的位置，其余位置需要涂的颜色都为 ，则 为 。
- 否则，需要涂的颜色至少有两种， 为 。
第一种情况下，这个线段树节点对应的所有操作都是可选的；第二种情况下，颜色为 的操作可选；第三种情况下都不能选。
涂色操作是好维护的，直接暴力修改颜色就行，如果遇到 是 0 的节点就不用往下搜了。
用一个队列维护一下类似拓扑的过程即可。
注意 存在 0，这种情况特判一下，显然所有操作不能覆盖这些位置中的任意一个。
T4-魔法对轰（apollyon）
题面
阿狸有 块符文，他将符文排成一排，并按照从左至右的顺序依次标号为 。每块符文都有对应的魔法值，第 块符文的魔法值为 。
由于虚空法术的侵入，有 块符文的位置已经无法改变了，这些符文的标号分别为 。
阿狸可以对除了标号为 的其余所有符文进行重新排序，使得在排序之后，对于每个 ，从左至右第 个符文的标号仍然为 。
阿狸希望用这 块符文组成一个魔法阵。具体地，假设在重新排列后，从左到右第 块符文的魔法值为 ，则魔法阵的法力消耗值为
阿狸希望在重新排列后，魔法阵的法力消耗值尽可能地小，以更好地与虚空法术对抗。输出这个最小可能的法力消耗值。
。
题解
首先有 ，所以题目相当于求 的最小值。
考虑 的做法，显然是把 从小到大排序然后算答案。
如果 ，那么相当于把原序列分成 段（这里对段的定义是：没有被卡住的瓷砖组成的极长连续段），然后在段内填数。同样，对于每段的内部，从小到大、或者从大到小排序一定是最优的。
为了方便，把 中所有没被卡住的瓷砖的丑陋值拉出来，排序，存在 数组中。
而对于一个单调不增、或单调不降的数列 ，有 。所以对于某一段，假设这一段前面一个被卡住的瓷砖的丑陋值为 ，这一段后面的那个为 ，段内首个瓷砖的丑陋值为 ，最后一个为 ，则这一段对答案的贡献为 。
可以看到，某一段对答案的贡献只与 有关。而 是固定的，所以我们接下来的算法中只需决策选择哪些数列 。
以下归并所有 的情况，并转化为 ，相当于把段进行一次翻转，这样操作不影响其他段。
可以证明，选择的这些数列 对应的线段 要么无交，要么为包含关系。
考虑反证法：在 的时候，段内的元素一定是单调不降的。那么，当 变大时，或者 变小时， 的值不会变大。如果存在选择的两个数列 满足 ，则交换 一定不劣。
考虑怎么实现这个选择数对的过程。注意到 的范围都不是很大，区间 似乎是可行的方向。为了方便，以下记录 表示 集合内所有段的长度总和。
设 表示在 区间内选择集合 内对应的所有段所需的最小代价。有转移方程如下：
表示把 这个集合的答案拆成两部分计算。
表示选择 作为编号为 的段对应的数对。
模拟赛题解/2025.10.23 模拟赛
· 阅读需 8 分钟
T1-Wei 子与 Runs（runs）
题面
Wei 子现在得到了一个仅由小写字母构成的字符串 ，他把每一个极长连续相同字符子段称作一个“段”（runs），他现在想问你有多少种不同的排列这个字符串的方案使得新的字符串段数和 相同。
由于答案可能很大，答案对 取模。 我们定义两个字符串 不同当且仅当 。
。
题解
先记录下每种字符出现数，记为 ，搞个前缀和 。
直接设 表示考虑了前 种字符，有 个连续段的方案数。
转移闭着眼睛整，枚举当前字符有多少段加在原来连续段间（加一段连续段数 +1），多少段在连续段中（加一段连续段数 +2），瞎乘个选择插入位置数，分配字符方案数了事，式子如下：
时间复杂度 。
T2-Wei 子与工厂（factory）
题面
Wei 子现在雇佣了 个工人给 台机器做工，每台机器都需要恰好一名工人来操作，才能保证工厂正常运转。
在招聘时 Wei 子得知 ，第 个工人是否会操作第 台机器。
每天，工人都会以随机顺序到达工厂并随机选用当前没有人使用且他会操作的机器开始工作。
Wei 子现在可以花费 1 元钱培训 1 个工人学会操作 1 个机器。
作为大资本家，小 W 不希望出现工厂无法运作的现象，现在他问你最少花费多少元钱使得无论如何工厂都可以正常运转。
。
题解
显然把工人和机器的关系视作一个二分图。
考虑这个二分图合法必然满足任意匹配都可以得到一组完美匹配。
考虑什么样的二分图是合法的。
可以发现必须每个连通块都满足两部分点数相同且是完全二分图。
充分性显然，必要性考虑反证，假设存在一个不符合我们上面条件的二分图但是合法。
我们在一个连通块 内找两个没有直接连边的左部点和右部点 。
考虑去掉这两个点后的图。
如果还有完美匹配，直接用这个匹配，此时 均无法匹配，爆掉了；
否则根据 Hall 定理，去掉 时左侧必然存在一个点集 使得和它相邻的右部点集 大小比它小，由于 联通， 中必然有点和 外的点相邻，直接将这样的点和 外点匹配掉 就爆掉了。
好的现在我们再来看题目要我们做什么。
原来有连边的部分必须分在一起，即你有一些左右部点数对 ，你需要把它们拼成左右部点数相同的点对，代价是单边点数的平方和减去边数。
此时直接开搜，对剩下点数对记忆化，每次暴力枚举一些集合合成一个左右部点数相同的点对即可。
可以发现本质不同状态数是少的，最坏 43008 个，可以通过。
T3-Wei 子与钥匙（key）
题面
有 个箱子，每个箱子都只能用某种特定类型的钥匙打开，打开后那把钥匙就不能使用了，箱子中可能放着一些钥匙，打开后你就可以获得该箱子内的钥匙。
现在你初始有 把钥匙，问你可不可能打开所有箱子，如果可能，输出字典序最小的打开所有箱子的方案。
这里，我们称一个方案为一个 的排列 ，使得我们能够按照编号 的顺序依次打开箱子。
。
题解
注意到我们本质上是要在知道我们当前有哪些钥匙，有哪些箱子的情况下判断是否有解，构造最小化方案只需要我们枚举当前开哪个箱子后判断剩下箱子是否有解即可。
考虑你最开始有一把钥匙，每个箱子内恰好有一把钥匙的情况。
把钥匙的种类视作点，一个箱子视作开箱子类型钥匙和打开后获得钥匙之间的边，题意就变成了指定点出发欧拉路径。
但是如果一个箱子里有多把钥匙，问题就不是欧拉路径了，考虑寻找一个图有解的情况：
-
当每类钥匙的总数大于等于需要使用的数量，且可以获取需要用的每种钥匙（上图从最开始拥有钥匙对应节点 BFS 可达），我们声称这是必然有解的。
-
必要性是显然的，充分性就是我们要说明始终存在一个可以打开的箱子，打开后不影响连通性。
你当前图满足：
对于任意需要的钥匙类型 ，存在一个钥匙种类序列 ，其中 为你当前手上拥有的钥匙，， 可以通过 打开的箱子获得。
考虑你手上的某种钥匙 ，如果你当前拥有数量已经超过需要数量了，显然无影响，否则：
你现在有一个序列 。可以获取一个 ，我们约定 。
- 若 ，则有：
对于需要的 钥匙，你现在有一个钥匙种类序列 可以获取 ，如果序列 中没有 ，使用后不影响连通性，否则你考虑找到最大 使得 使得 ，若你使用了 ，你现在可以使用 获取 。
- 若 ，则有：
直接用 获取 ，你发现 论证仍然成立。
故上述条件充分。
做就直接枚举当前位于哪个箱子，去掉这个箱子后在剩余图上 BFS 即可，时间复杂度 。
T4-Wei 子与串串（string）
题面
Wei 子现在收到了一个长度为 的匹配括号串 ，作为图论带师，他凭借这个括号串构想了这样一个带权有向图：
有 个节点，点 和 之间互有连边，若 和 是匹配的，则 之间互有连边。
为了评估这个图的复杂性，他现在问你 次从他给出的起点 走到 的最短路是多少。
。
题解
将括号串建树。对于一个满足左右端点匹配的区间 ，建一个虚点 并建立 。再递归推出 区间内的若干不交匹配区间的子树，将 连向这些子树的根节点。最后再建一个虚点将建出来的森林的根连起来。
对于一组询问 ，考虑求出 在树上的 LCA 。求出 使得 是 的儿子，且 分别在 的子树内。
令 表示一个结点 所代表区间的左、右端点。显然 的路径一定满足 。
现在的一个问题在于求出一个结点儿子之间的最短路。情况如下图。
如果边权皆为 1 我们就容易用前缀和得到答案。否则就需要将所有匹配括号 间的边权更新为它们之间的最短路才能保证正确性。这个可以在树上从下往上再从上往下转移。
接下来我们只需要求出一个点到其某个祖先（或者反向）的最短路。设 表示起点为 或 的 级祖先， 结点的左/右端点与 的 级祖先的左/右端点的最短路，可以倍增转移。
模拟赛题解/2025.10.20 模拟赛
· 阅读需 7 分钟
T1-染色（color）
题面
有一个长度为 的序列 ，你需要对这个序列进行染色。定义一种染色方案为，对于序列中的每个数赋一个大小在 范围内的值，且不能赋值为 。
小 P 认为染色后 序列价值为 。小 Q 认为染色后 序列价值为 。
现在你需要找出一种染色方案，使得小 P 认为的价值和小 Q 认为的价值相等，并且不为 ，请你输出这样的一种染色方案。
可以证明，在本题给定的数据范围下，保证所有数据均存在一种染色方案。
形式化的，即你需要找到出一个长度为 的非零整数序列：。
。
题解
考虑先钦定前 位，然后直接得出 的值。
注意到乘法会使值的增长速度很快，所以乘法要尽量 ，考虑用 和 构造。
于是钦定 ，可得 ，一定有解。
T2-超速检测（detect）
题面
由于小 D 被大运创飞了，上司派小 P 重新设置检测点。
有 辆大运，第 辆大运从 处进入国道，从 处离开。
大运在行驶过程中，全程超速。小 P 想知道至少要设置多少个检测点，使得每辆大运都会被检测到超速。
具体地，在 点放置一个检测点，可以检测经过 区间的大运。
同时，小 P 不想被创飞，所以他也想知道所有的使得检测点最少的方案的数量，以备不时之需。你能帮帮他吗？
由于方案数过大，请输出对 取模后的结果。
。
题解
令 表示强制选择第 个点的最小值， 则表示方案数。发现前面如果有一个区间 没有被 覆盖则 。
上面这个 dp 显然是可以线段树优化的，时间复杂度 ，常数较大，期望得分 80 100 分。
并且注意到 单调不降，所以 的时候一定最优，而这个 可以通过单调队列维护，注意需要合并相同的 用来统计方案数，时间复杂度 。瓶颈在于排序，期望得分 100 分。
T3-决斗（duel）
题面
小 P 在和怪兽决斗，它们在一个 个点， 条边的有向图上，小 P 在起点，怪兽在终点，小 P 要去打败怪兽。
小 P 相信玄学，所以他必须经过正好 条边，再去打败怪兽。同时，小 P 在路途中，不能回到起点，也不能到达终点。
他想知道他有多少种去打败怪兽的方法，答案对 取模。
。
题解
设 表示从 出发，恰好走 条边，最终走到 的方案数。 表示从 出发，恰好走 条边，最终走到 且路径中间没有经过 的方案数。 表示表示从 出发，恰好走 条边，最终走到 且路径中间没有经过 的方案数。
则有：
时间复杂度 ，期望得分 100 分。
T4-擂台游戏（arena）
题面
小 P 要举办一场擂台游戏，这个擂台上有 个依次排列浮岛。开始时，小 P 会决定这些浮岛的沉浮状态。 表示浮， 表示沉。
游戏开始后，对于每一轮，选手可以选择两个相邻的浮岛使它们的状态全部变为浮。在选手选择结束后，小 P 可以选择任意三个浮岛使它们的状态全部变为沉。若浮岛数量不足三个，也可以选择小于三个浮岛使它们的状态全部变为沉。
当所有浮岛全部为沉时，选手就会掉进岩浆，游戏结束。
小 P 想知道，当双方都采取最优策略时，选手最多可以存活的轮数。
。
题解
算法一
由于所有的状态数只有 种，所有可以直接记忆化所有状态，时间复杂度 ，期望得分 20 分。
算法二
特殊性质 A：这个时候，选手可以贪心地先选择所有编号为奇数的浮岛，这样小 P 每次只能消除一个 1；直到选手只能往 1 空隙中改变状态为止，时间复杂度为 ，拼上算法一期望得分 40 分。
算法三
考虑选手的每次将相邻浮岛的状态变为浮的过程，按照时间推移，这个过程形如：
- A 部分：若干次连续消除两个 1。
- B 部分：若干次消除一个 1。
- C 部分：若干次连续消除两个 1。
因为 A 部分和 C 部分每次都是后一轮比前一轮多一个沉的浮岛，所以说我们只需要计算出 B 部分的轮次数就是对的。
对于 A 部分：先贪心地模拟选手，每次消掉两个连续的 1，并直接算出它所需要的轮次。在 A 部分，显然小 P 的最优策略是在保证任意两个 1 不连续的前提下，尽可能的使更多的浮岛的状态为 1，这个部分可以用 dp 求解。
考虑 B 部分应该怎么做：由于选手每次都会采取最优策略，所以说小 P 每一次将选手设置状态为 0 的浮岛的状态重新设置为 1，这一定是最优的。
但是这样会存在一些特殊情况，即不管怎么样选手第一轮无论怎么选择都比较劣，形如 010000001000，这种情况可以直接扫一遍判断。对于剩下来的时间，每一轮小 P 显然每次可以增加 2 个状态为 1 的点，所以也是好做的。
在 A 和 B 两段都做完的情况下 C 段可以直接求解，时间复杂度为 ，期望得分 100 分。
的部分留给知道整个过程是怎么做的但是暴力枚举的选手，特殊性质 B 给一些正解少判了情况下的选手。
模拟赛题解/2025.10.18 模拟赛
· 阅读需 11 分钟
T1-大水题（water）
题面
栋栋给定一个字符集为 的字符串。
现在你可以执行以下 种操作任意次：
- 选择任意一个 ，将其替换成 或 。
- 选择两个相邻的 ，将其删除，并连接剩下的字符串。
- 选择两个相邻的 ，将其删除，并连接剩下的字符串。
请帮栋栋求出可能得到的字符串的最小长度。
。
题解
我们发现 和 要分开来讨论很烦，但是注意到一个性质：
每次删除都是两两进行，所以删除后每个点的奇偶性不变，两个能被一起删除的点一定是奇偶性不同的。
所以考虑直接把所有偶数位取反，问题就变成了可以删除一对 或 ，把 视为 ，则可证和为零的区间一定能被消除。
所以直接计算除了 之外的总和，用 尽量去降低总和的绝对值（即最终剩下的字符串长度）即可。
时间复杂度 。
T2-大水题（water）
题面
对于正整数序列 ，栋栋定义 为最大的 使 可以被划分为 个连续子段， 使任意两段元素构成的集合无交，即任意两段没有相同的元素。
如序列 可以被划分为 这 段，且没有更优的划分方式，所以 。
现在要求你对于任意长度为 ，值域在 中的正整数序列 求出 之和。答案对 取模。
。
题解
对于给定的序列，划分方法是显然是，直接从左到右贪心进行即可。
Subtask 1
枚举序列，然后线性求答案。
Subtask 2
只能等于 1 或 2。简单算出 的情况数，然后就能算出答案了。
Subtask 3
总贡献问题，考虑对贡献算方案。关键是，你的贡献是什么。如果以一个段为贡献，能引导出一些做法。
考虑对于一个段，我们如何确定包含它的序列个数。首先要求这个段不能被分隔成若干小段，不然肯定会算重。其次我们需要知道段的长度和种类数。假设其长度为 ，种类数为 ，包含它的序列个数为：
接下来要求长度为 ，种类数为 的不可分割段的数量，设为 。考虑容斥，以第一个不可分割段区分方案。
将 乘上方案就可以算答案了，注意每个种类还需要分配一个具体的颜色。种类数一定不超过序列长度，第二维实际上是 级别，时间复杂度 。
Subtask 4-5
有 的做法，但是难度远大于正解，也和正解没关系，不多说。
Subtask 6
依旧枚举贡献，但是这一次不以段为贡献，而是以分段点为贡献，因为 也等于分段点的个数。考虑求 的过程，什么样的点可以分段？一定是 和 无交的 可以作为分段点，这个也是非常容易理解的。所以我们直接计算 作为分段点的方案。
同样的， 的范围实际是 。时间复杂度 。
T3-送分题（score）
题面
小 X 喜欢思考关于最大前缀和的问题。她认为一个长度为 的序列 的最大前缀和为 的最大值。
同时，她喜欢用 表示序列 的连续子序列 。
小 X 有一个长度为 的序列 和 次询问，每次询问给出 。对于每次询问，她想要知道 的所有连续子序列的最大前缀和的和。
由于小 X 无法与你直接交流，她的询问将以一种特殊的方式给出，你的回答也需要以特殊形式输出。具体见输入输出格式。
。
题解
首先，处理出前缀和数组 ，区间 的最大前缀和即为 。
对于询问 ，要求 的最大前缀和。其中 的项是容易预处理前缀和然后 计算的。只考虑后面的一项，问题就成了任意子区间最大值的和。
时间复杂度 。
关键词：扫描线，历史版本和。
在从左往右扫描右端点 的过程中，是容易使用单调栈 + 线段树 维护出每个左端点 的答案的。每个询问会查询 ，对于 是查线段树上一个区间， 则用历史版本和差分得到。需要写主席树。
时间复杂度 或。
先考虑 ，即询问区间的所有后缀的贡献。
模拟一个左端点 ，然后往前移动的过程。过程中维护最大值，并贡献答案。
对于每个点，找出其左边第一个大于它的点。这样的关系构成了树。并且上述过程中最大值的变化过程构成了一条向上的链。记 最大值为 ，则这条链从 开始，到 结束。发现链上的点，除了 之外点的贡献是可以预处理的，点 的贡献为 。于是可以预处理树上前缀和之后再差分，对于 的贡献单独处理。于是 的部分贡献为
发现对于 的部分，贡献只与最大值有关。仔细思考一下，在解决一个 的问题时，也可以视作只关注了最大值处，所以理论上，解决单个区间的复杂度与解决后缀区间的复杂度是几乎一致的。之前的问题相当于计算每个后缀区间的"单个区间"之和，之后的问题相当于计算每个前缀区间的"后缀区间"之和。
聪明的你想必不再想听到重复的过程了。
于是只需要求出区间最大值的位置，就可以 计算答案了。
用 ST 表预处理带 ，用一些高级的东西就可以线性了。
T4-计数题（count）
题面
栋栋有一个下标为 的序列 ，我们并不知道 中任意一个元素的值。
给定在 上建立的一棵广义线段树。对于线段树的每个非叶子节点 ，设它管辖 。它有一个属性 表示其左儿子管辖的区间为 ，其右儿子管辖的区间为 。规定根节点管辖的区间为 。
容易发现这棵线段树有 个非叶子节点和 个叶子。
定义一个区间 的权值为 。
现在给出 个区间 。易知这棵线段树节点的子集共有 种，请你求出其中有多少个集合 满足：如果已知 中所有节点的管辖区间的权值，则 个区间的权值都能唯一确定。答案对 取模。
区间 的权值能唯一确定指：存在某种运算已知区间权值的方法，使得到的一定是 的权值。
例如：已知 的权值，就能确定 的权值。已知 的权值，就能确定 的权值。然而知道 的权值并不能确定 的权值。
。
题解
性质1：将 中的区间 看成一条 间的无向边，那么 能被唯一确定当且仅当 连通。 表示增加这一部分和， 表示减少这一部分和，一条路径一定对应一个能确定的区间。
Subtask 1&2：
枚举 ，然后连边判断连通性即可。时间复杂度
Subtask 3：
考虑在线段树上做树形 DP，决策当前节点是否选择。考虑在 的 处匹配它们。
需要两种状态：
表示 连通，且 子树内未匹配的单点都与 中的一个连通。
表示 不连通， 子树内未匹配的单点是与 还是 连通。
如果有一个未匹配点不与 或 连通，那它将不可能去到 以外的结点，一定无法和另一个点匹配，是一个非法的状态。
直接转移，视实现应该是一个和 到 之间的算法，可以通过。
Subtask 4
真的需要找正每一个单点是和 还是 连通吗？
性质2：如果 不连通，则 内和 连通的节点都在和 连通的节点的左边：
既一定是上图的情况。如果是下图的情况，说明 直接连通。感性理解一下，一条连边其实将内部划成一个封闭的区域，内部的点想出去一定要和端点连通。
同样需要两种状态：
表示 连通，且 子树内未匹配的单点都与 中的一个连通。
表示 不连通，最后一个与 连通的点的位置是 。且 的未匹配的单点都与 连通， 的未匹配的单点都与 连通。
考虑转移：
首先是 连边的情况：
（增加不连通段， 中所有未匹配的单点都是连通的，要求 中不存在匹配点在 之外的点）
不连边的情况：
（增加不连通段， 中所有未匹配的单点都是连通的，要求 中不存在匹配点在 之外的点）
暴力做这个 DP 就是 的。
Subtask 5
性质 3： 可以转移当且仅当跨过 和 的询问区间集合相同。证明显然。
所以可以先用和哈希，把下标分类。直接用下标等价类代替 的第二维。
现在的 DP 就是 左边乘系数 + 右边乘系数 + 左右对应位置乘。显然 里有值的点只有 个，哈希表启发式合并即可。
时间复杂度：。
模拟赛题解/2025.10.17 模拟赛
· 阅读需 9 分钟
T1-二分图（graph）
题面
对于一个二分图，设 为左部点的一个非空子集，定义 为右部点与 相邻的点的点集。
若 ，则称 是好的。
请你构造一个二分图，使得左边有 个点，右边有 个点，且恰好有 个好的子集。本题每个测试包含多组输入数据，你需要分别独立处理每组数据。
。
题解
考虑让左部点每个 连向右部点的一个前缀 ，满足 且 。
此时，以 为最大元素 的 都等于 ，好的 有 个。
从大到小考虑每个 ，选择最大的 使 减去最大元素为 的方案数后 ，递归进入子问题。
要证明在这个过程中时刻满足 。因为有 ，所以 。而 等价于 在处理到 时，要求 ，化简后 ，成立。
T2-乌龟与 ABC（string）
题面
乌龟正在学习英文字母。
为了训练乌龟的拼写能力，小猪给了乌龟一个由字符 A、B 和 C 组成的长度为 的字符串 。
乌龟可以对 进行若干次操作。一次操作可以进行以下三种操作之一：
- 选择 中的一个等于 AB 的子串，将它替换成 BA；
- 选择 中的一个等于 BC 的子串，将它替换成 CB；
- 选择 中的一个等于 CA 的子串，将它替换成 AC。
请你告诉乌龟他最多能进行多少次操作。
。
题解
字符串里的每个元素，只会和同一种字符交换。例如当交换 AB 后，别的 C 不可能到达 BA 之间，所以此时这个 A 和 B 永远不能和 C 交换。
所以要将字符串划分为若干段，每段至多包含两种字符，该段内的这两种字符进行交换。交换的最大次数即``逆序对数''。
设 表示划分完前缀 的最大次数。可以通过维护每个 B 之前有多少个 A，以及相关前缀和，得到可以斜率优化的区间贡献的形式。
还可以更进一步，合法的转移点是 的。
每个划分断点两侧的字符都应当不同，每个相邻的段的字符集合都应当不同。对于每个 ，双指针维护最小的 j 满足 只有至多两种字符，则可以划分为新一段的位置是 j 所在的极长同字符连续段的两端。
复杂度线性。
T3-跳伞（skydive）
题面
有 个跳伞者，每个人身上系着一段由 ( 和 ) 组成的绳索——每段绳索就是一个长度为 的括号串。
我们可以把这些绳索以任意顺序首尾相连，形成一根更长的绳子，然后把所有跳伞者一起从飞机上放下。绳索里每一对能“配对消失”的 ()，就是一次安全的折叠与收回。
但现在我们的目的正好相反。为了考验着陆控制，飞机故意想把绳索弄得越乱越好，于是它会把这些绳索以某种顺序连接，使得最终长绳上能被重复删除的 () 对数尽可能小。
在此前提下，我们定义长绳上能被重复删除的 () 对数为这个局面的权值。例如：
- 若长绳的串为
)(()(，局面的权值为 ； - 若长绳的串为
(()))())，局面的权值为 。
现在跳伞者们还不知道他们身上的绳索是什么。他们想知道，如果他们身上的绳索都是一个每一位等概率随机生成的长度为 的括号串，局面的权值的期望，对 取模。
题解
考虑给你 个括号串怎么做。经过一些推导，不难发现答案是：
其中 和 分别为第 个串的左括号和右括号数量， 为把括号串视为网格图上的折线，起点与最低点的距离， 为终点与最低点的距离。
前者是容易的，枚举每个括号串有多少个左括号即可。答案为：
后者考虑拆贡献，计算：
所以我们考虑先枚举 ，对单个 算 的方案数。
将最低点设为 0，要求就是起点和终点都 。考虑枚举起点 ，终点 。最低点恰好为 0 可以容斥掉，即方案数等于经过 的方案数减去经过 的方案数。
所以固定 的方案数为：
答案即为：
发现固定 后正负号抵消，上述式子等于：
这个很明显是组合数后缀和的形式。所以在最外层枚举 ，预处理组合数后缀和，即可 求出上述式子。
时间复杂度 。
T4-乌龟与游戏（game）
题面
乌龟正在玩一款在线多人对战游戏，玩家们操控自己的角色进行较量。
假设有 名玩家参加一场比赛，我们依次将他们编号为 1 到 ，第 名玩家的角色初始体型为 。
在游戏中，第 名角色可以攻击第 名角色（）的条件是：。
其中 是比赛开始前设定的一个整数参数，可能因比赛而异。
当一次攻击发生时，第 名角色会被淘汰，而第 名角色会吸收它的能量，使自身的体型变为 。
比赛会持续进行，直到场上再也没有可能的攻击为止。
如果最终只剩下一名玩家存活，则他成为本场比赛的胜者。如果存在一种攻击顺序，使得一名角色可以成为本场比赛的胜者，则称该角色是潜在赢家。
为了训练乌龟的游戏能力，小猪给了乌龟一个长为 名玩家的初始体型，由数组 表示。 接着，小猪向乌龟提出 个问题，每个问题如下：
- 若选取区间 中的角色进行一次比赛，并设比赛参数为 ，那么这场比赛中有多少名玩家是潜在赢家？
请你帮助乌龟解答这些问题。
。
题解
考虑判定一个人是否能获胜。则他会每次选择生命最小的人尝试吃掉，如果不能吃掉某个人就无法获胜。
将区间按生命排序。显然一个后缀的人能够获胜，每次会吃掉的是一个前缀。每个前缀会对能够获胜的最小生命值要求有限制。
设初始的人为 。对于一个 ，要求 。对于每个 ，要求 。暴力复杂度 。
记 。如果存在 ，则 翻倍，只会出现 次。但翻倍的性质只有 时存在，不过 时一定不合法，二分最小的 使得 并从那里开始。
同理处理第二种。在 时处理 次，但在 时的取值无法求出。记 ，因为 时 ，所以只需要考虑 的情况，因为 ，只用考虑 次。
主席树维护。复杂度 。
模拟赛题解/2025.10.16 模拟赛
· 阅读需 6 分钟
T1-签到题（easy）
题面
给定长度为 的数组 和长度为 的数组 ，构建大小为 的网格，其中单元格 中的值为 。
从 (1, 1) 开始，每一步都要选择一个位于右下方的网格单元格进行移动，直到到达 ，目标是最大化路径上相邻单元格之间的绝对差值之和。
从形式上看，您的目标是找到满足以下条件的序列 ：
同时使 最大化。
。
题解
相邻两个不同的限制是无所谓的，因为对答案没有影响。又因为根据绝对值的性质，有 ，所以可以发现每次往右或往下走一步是最优的。
而由于权值 ，所以 实际等于 或 ，并且无论路径如何，答案都等于 ，故直接输出即可。
时间复杂度 。
T2-简单题（simple）
题面
给定一棵 个点的树，问有多少个非空路径集合，使得集合内的路径的点集的交非空，答案对 取模。
在本题中，我们认为路径的两个端点不能相同，且我们不区分端点的顺序，即路径 和路径 我们认为是一样的。
。
题解
考虑到路径的交一定是一条路径，于是想到点减边容斥，于是只需要单独考虑所有点和边，计算被所有 路径覆盖的方案即可。
时间复杂度 。
T3-入门题（basic）
题面
定义一个序列 是好的当且仅当满足以下条件：
对于一个序列 ，定义
求所有好的序列的 之和，对 取模。
在本题中，我们认为 。
。
题解
Sub 2
记 表示当前序列长度为 和为 ，最后一个数为 的权值之和。
复杂度 。
Sub 3
记 表示当前序列和为 ，最后一个数为 的权值和。
复杂度 。
Sub 4
注意到，序列长度和值域不能同时太大，于是考虑按 的大小分类。
记 表示最小的使得 的数。
若 直接跑 的 ，复杂度 。
若 则不用考虑 的限制，约定 ，枚举长度后直接跑 的 。
总复杂度 。
Sub 5
考虑优化 部分的 ，为了第二部分可以不计最后一个数是多少，于是考虑倒着加数，由于我们确定了 ，于是往前加一个数的贡献就是整体上移或下移，于是可以优化到 。
T4-送分题(freebie)
题面
小 A 和小 B 将玩一个游戏。
初始时，有一个可重集，每轮开始时，双方各选择一个元素，但是双方都不知道对方的选择。
若双方的选择相同（注意，并不是指值相同。如 ，我们认为选择第一个 1 和选择第二个 1 是不同的选择），则将这个元素删除。此时，若可重集内没有元素，则游戏结束，否则，继续下一轮。
若选择不同，则小 A 得到这个元素的值的分数，并结束游戏。
小 A 想让自己的得分最大化，小 B 想让小 A 的得分最小化，若双方都足够聪明，求最终小 A 得分的期望。
相对或绝对误差小于 则视为正确。
，可重集内元素 。
题解
首先，小B的策略一定是基于概率的，即对于一个局面，小B会对于每个物品都有一个概率表示当前局面下选这个物品的概率，然后按概率随机选择一个。
考虑状压 DP，令 表示还剩 以内的题没被选中时你的期望得分的最大值，不妨令 表示除去 题后期望得分的最大值，即 ， 表示小B选中第 题的概率，那么有转移：
不妨将 从大到小排序，其一定满足 ，先让所有 ，令 表示当前的 ，那么初始有 ，接下来一步步调整 ，看 能取到的最小值，如果某个时刻 ，那么撤回这一步骤作，将 平均分配到前面这些 中。如果有 ，那么 的最小值只能是 。
直接模拟上面的过程即可，时间复杂度 。
模拟赛题解/2025.10.14 模拟赛
· 阅读需 7 分钟
T1-共同好友（A）
题面
社交网络可以看做一张图，每个人为一个结点，如果 人互为好友则连一条双向边。
在社交网络应用中，一个常见的问题是询问 个人的共同好友数量，请你解决这个问题。
。
题解
本质上就是无向图三元环计数的运用，考虑根号分治，度数 的数用 bitset 预处理，其他点直接暴力跑。
复杂度为 。
T2-操作序列（B）
题面
有 个变量 ，初始值都为 0。
依次给出 个操作的信息，操作分为 2 种：
-
：代表将 的值加上 ；
-
：代表将所有变量的值乘 ；
所有运算在 下执行。
现在给出一个操作序列，请问依次执行序列中的所有操作之后，每个变量的值是多少。
具体的，操作序列以 个区间 的形式给出，依次执行每个区间、每个区间按编号从小- >大执行区间内的操作，即完整的操作序列为：
- 。
。
题解
记第 个区间的乘法次数之和为 。
对于某次加法操作 ，其最终贡献取决于它之后的所有乘法操作次数 ，可以将 看成由 部分组成：
- 对于所有包含 的区间 ，之后所有区间的乘法次数之和 。
- 对于所有包含 的区间 ，区间内 中的乘法次数之和。
从 遍历所有区间，维护一个倒序差分数组 ，对于第 个区间：
- 在 处加上 ；
- 在 处减去 ；
从 遍历所有操作，维护一个变量 ，由差分数组 可以求出第一部分 ；每次遇到乘法操作让 乘 就可以正确处理第 部分区间内的贡献。
复杂度 。
T3-AND和XOR（C）
题面
给定 个整数 ，在这 个整数中选出 个（），使得 个数的按位 and 和恰好等于按位 xor 和。
种方案不同当且仅当选出的 个数的下标集合不同，请你求出不同的选择方案数，对 取模。
。
题解
首先有 的暴力DP，滚动之后空间是 ，可以得到 分。
观察到每位只有3个状态：全为 ，或者有奇数/偶数个 。 可以预处理 其三进制表示。 记 DP 状态 前 个数已经选了奇数/偶数个数，每位的状态是 的方案数，枚举 选或不选进行转移，复杂度 ，滚动之后空间 。
考察我们实际上求了什么：设 表示在所有 的 中选出一个大小为奇数/偶数 的子集，异或和为 的方案数，我们最后要求的是 。
先枚举 ，设 表示所有 的 组成的序列，布尔数组 表示所有每个 有没有被选，发现选奇数/偶数个和异或和的都限制可以被一个异或方程组刻画。
枚举每一位 ，设 表示 的第 位，则 的限制为：
和其本质相同。 对其做高斯消元，若无解方案数就是 ，否则就是 ， 为消完后的矩阵非 行的个数。
直接做是 的，期望获得 55 分。
发现由于矩阵只有 ，所以可以把每行存到一个 bitset 里优化高斯消元，复杂度除以一个 ，可以获得 分不等。
到这时候你会发现你把线性基给忘了，而线性基的经典应用——求 个数选出异或和为 的子 集的方案数，和上面的高斯消元是等价的。 具体地，我们先把每一个 增加一个恒为 的位，这里使用了 ，这样如果我们要求选奇数个异或和为 ，就变成了选异或和为 的子集。于是这个问题就直接可以用线性基解决。
具体地，将修改后的每个 插入线性基，设 为插入失败的 个数（即 能被已经插入的 数表示出来）。则 ；若 能被表示，，否则为 （简单来说就是 个数可以随便取或不取，最后再用插入成功的那些数唯一地组合出 ），具体证明可 以自行上网查找。 复杂度 ，期望获得 80 分。
每次枚举 挨个加入每个数太蠢了，考虑 的线性基里面是 的超集形成的线性基，所以我们直接可以用类似高维前缀和的方式进行 次合并，每次合并是 的，所以加上每个值插入的复杂度，总复杂度是 ，常数很小。
T4-朝日（D）
题面
定义素数导出序列为一个序列 ，其中每个元素都是素数，且单调不降。
若把所有素数导出序列，按照序列中元素和作为第一关键字，序列中元素个数作为第二关键字, 序列的字典序作为第三关键字排序。将所有素数导出序列从小到大排序后取前 个序列组成 的数组,每个序列是一个 vector，所有序列按照顺序放进一个 vector 里面，输出这样一个 C++ 源码可以用于打表。
现在请你输出这个表的第 个字符到第 个字符。
。
题解
考虑令 为第 个素数以后构成的、序列和为 、长度为 的素数导出序列个数。
为第 个素数以后构成的、序列和为 、长度为 的素数导出序列对应的字符串的总长度。
显然我们可以递推 ，这是一个基础背包。 考虑复杂度，根据计算发现，第 个字符大约是在和 的时候取到，所以总状态数有 个，可以通过。
那么我们每次想知道一个字符，只需要像 50分一样，大力 DFS，根据 判断下面的分支的大 小，进入适当的分支，就可以了。
模拟赛题解/2025.10.13 模拟赛
· 阅读需 7 分钟
T1-接雨滴（glory）
题面
Moon 发现自己来到了一个二维平面上，但是自己只能在 的直线上以不超过 的速度行走（可以折返来回行走）。这个时候天空开始下了倾盆大雨，一共有 个雨滴，第 个雨滴以 的速度从 开始匀速下落，同时开始刮起了速度为 ，方向为 轴正方向的大风，可以认为每个雨滴在水平方向上有了和风速一样的速度，以及风不会影响人的行走速度。
Moon 非常喜欢淋雨，为了简单起见把每个雨滴和 Moon 都视为是一个点，只有某 个雨滴到达 轴的位置的同时，Moon 也正好在这个位置上，Moon 才可以被这个雨滴淋到。现在给出 个询问，第 次询问给出一个初始位置 ，Moon 想知道自己从 出发，在整个运动过程中，最多可以被多少个雨滴淋到呢？
。
题解
我们考虑雨滴不动而人去动。可以发现，一个人在 处一秒内能走到的位置是 到 。那么，我们离线下来每个点，然后从每个 点出发画两条方向为 和 的射线，这两条射线围起来的面积就 是从这个点出发能够到达的所有点。
由于所有点出发的两条斜线斜率分别相同，所以我们改变坐标系，将这两条斜线当作 轴，就变为了一个二维偏序问题，离散化后树状数组维护。复杂度 。
T2-验题（verify）
题面
由于原题机爆炸了，小 被迫当起了人肉原题机。
小 的记忆里有 道题，按印象从深到浅依次编号为 到 。初始时，有 对题 在小 思维中存在联系，第 对联系连接 。
然而，沿联系 dfs 搜索对小 的消耗很大，因此他需要增加一些联系来减少搜索 的深度。具体的，小 每次会从一个印象较深的题 ，沿联系想到两个印象浅的题 （，、 间有联系， 间没有联系），并在 间添加一对联系。小 会不断进行上述操作直到没有联系可以添加。
但过多的联系会使小 的大脑爆炸，因此他想知道最终题目间有多少对联系。
。
题解
一个简单的观察是以 从小到大的顺序操作能将所有可加的联系都加上，因为操作 时不会使小于 的题增加新联系，进而产生新的 操作。则有一个暴力的思路是从 到 枚举 ，将所有 连向大于 的点之间都加上联系，复杂度 。
显然两两暴力连接是没前途的。观察操作形式，发现枚举 时只要找到 连向的点 中最小的 ，并只添加 与其他 连向的点的联系，得到的结果与暴力相同，因为除 外的点之间未连接的联系会在 时进一步连接，直至最终全部被添加。
此时操作相当于将 与 向编号大的点连出的点集 ，并计算 点集中新增 的点数。使用启发式合并，可以做到 。
T3-颜色（color）
题面
给定一张 个点 条边的无向简单连通图。
给定正整数 。初始时，每条边的颜色均为蓝色，有一个棋子位于点 ，每次操作 你可以把棋子移动到一个相邻的点。
对于每 次操作，棋子在这次操作所经过的边会被染成红色。你需要构造一组方 案，使得每条边恰好被染红一次，或者报告无解。
。
题解
对于 的情况，就是欧拉路板子。
对于 ，如果图是一棵树，考虑一个欧拉序，不难发现每条边恰在奇数位置出现一次，偶数位置出现一次，直接输出即可。如果图不是树，可以拉出一个 dfs 树，每走到一个点就把与其相连的返祖边来回走一边。
对于 ，考虑直接在 的方案上扩展，例如，如果 下得到的边的序 列是 ，在 时可以变成 ，变换之后出现在 的倍数位置的和边在原序列上出现在偶数位置的边是相同的。
对于 ，每走一步后随便找一条边来回走即可转化为 或 。
时间复杂度 。
T4-字符串（string）
题面
给出一个长度为 的全部由数字组成的字符串 。在此基础上，进行 次询问。
对于第 （）次的询问，给出一个非空字符串 ，你需要找出一个最小的 （），使得 的字典序最小。对于每个询问，你只需要输出你找到的这个 即可。
。
题解
若 的字典序小于 的字典序则称 ，若 的字典序小于等于 的字典序则称 。
容易注意到如果答案是 则 。
而 。
考虑把 划分成 个段 使得 。
显然有多种划分方式，但是我们取 组成的序列字典序最小的。
易证对于查询串 一定只会在 与 之间插入而不会在 内部插入。
二分出在哪一段插入，用哈希加二分判 是否为真即可。
时间复杂度 。
注：发明出倍增排序查询串并使用双指针可以做到 。
模拟赛题解/2025.10.11 模拟赛
· 阅读需 9 分钟
T1-那头与艺术（art）
题面
那头现在有 种可以表演的行为艺术，第 种有一个特征值 （ 可能相同）。那头在一轮表演中会按某个顺序表演每种艺术恰好一次。我们称一轮表演构成了序列 ，当且仅当在这一轮表演中那头表演的第 项艺术的特征值为 。那头认为如果两轮表演构成的序列分别为 ，那么就会产生 的不优美度。现在那头希望你给他指定两种表演顺序，他将按这两种顺序各表演一轮。但是为了凸显艺术性，他将在第二轮表演之前任意循环左移你给定的顺序。现在，你需要最小化这两轮表演可能产生的不优美度的最大值，并给出方案。
形式化题意：给定长为 的序列 ，你需要构造 的两个重排 和 ，最小化 ， 其中 表示序列 循环左移 位得到的序列。
注： 表示序列 和序列 的最长公共子序列。
。
题解
首先特判掉 中所有元素相同的情况。
容易发现答案有一个下界： 中众数出现的次数加一。
具体的，记众数为 ，任意一个其他的数为 。那么 形如 。显然可以通过循环移位使得 中只包含 和 的子序列相等。 尝试构造取到这个下界。 一种构造方案是 为 升序排列后的结果， 通过不断降序取 中剩余元素各一个得到。 例如： ，则构造 。容易发现上述构造符合要求。
T2-那头与追忆（recall）
题面
在那头的记忆中，他曾经写过如下的代码：
#define ll long long
ll a[1000005],cnt;
void solve(ll l,ll r)
{
ll maxn=−1,id=0;
for(ll i=l;i<=r;++i)
{
++cnt;
if(a[i]>maxn) maxn=a[i],id=i;
}
if(l<id) solve(l,id−1);
if(id<r) solve(id+1,r);
}
现在那头给你一个长度为 的排列 ，并 次询问你，第 次询问给出 。你需要回答他，如果他将 设为 ，然后调用 之后 的值是多少。
。
题解
问题本质即为区间笛卡尔树所有子树 和。 考虑算 结点在整个序列的笛卡尔树 大小，考虑找到 左边第一个比他大的位置 ,右边第一个比他大的位置 ，分别记为 ，它的 即为 ，加上每次询问区间的限制 即为 。
分别做 ，这里以 为例： 离线做扫描线，对于 维护每个 （）此时的 ，按 排序，在 时单点修改即可。 是类似的。
时间复杂度 。
T3-那头与星铁（starrail）
题面
那头有 个头和 条通信线路，每条通信线路双向连接了两个头，并且有一个权值。由于那头认为排列是可爱的，所以保证通信线路的权值构成了 的一个排列。如果将那头的头和通信线路视为一张无向图 ，那么那头保证 连通且没有重边和自环。那头定义一张无向图 的关键森林 表示 中每个连通块的最小生成树的并集。
为了游玩《崩坏·星穹铁道》，那头需要改变自己。具体地，那头现在想要改变这些通信线路的权值，又不想改动关键森林，于是他要求你计数满足以下条件的无向图 的数量：
与 的点集与每条边所连接的点均相同，仅有边的权值不同，且对于边集的任意一个子集 ，设 在 中构成子图 ，在 中构成子图 ，那么有 。
那头很宽容，所以你只需要输出答案对 取模的值。
。
题解
考虑 合法的条件。有一个显然的充要条件是对于每个环， 中权值最大 的边与 中权值最大的边相同。
尝试刻画边之间的大小限制。按边权从小到大加边，设当前加入的边为 ， 那么限制 的边权大于加边后 所在点双中的其他所有边。
实际上，对于每个点双，取这个点双最新出现的边作为代表边，那么如果在 加入前 位于同一点双中，只需要限制 的边权大于这个点双的代表边。否则限制 大于 所在边双代表边和 所在点双代表边。
发现上述限制关系构成一棵森林。我们需要求该森林的拓扑序个数。根据经典结论，设 加边后 所在点双大小为 ，答案即为 。暴力实现上述做法复杂度 。
现在我们只需要动态加边维护点双。为了方便实现，可以先加入 G 的最小生成树上的所有边。动态维护圆方树，对于每个圆点 ，用并查集维护 的父 亲（一个方点）。设当前加入的边为 ，如果 是一 个方点，则把路径上所有方点合并到 ，否则合并到 。 找到路径上的方点只需要不断跳 中 较大的一个即可。
复杂度 。
T4-那头与串串（string）
题面
现在那头输出了一个长度为 ，字符集 的字符串 。由于你的 限制， 中每个字符最多会出现两次。现在你需要求出 的本质不同子串个数。
但是这也太板了！所以我们修改了一下本质不同子串的定义。定义子串 与 本质不同，当且仅当可重集 不等于可重集 。
。
题解
记 表示可重集 。对于每个 ，记 表示满足 的 ，如果不存在则为 。
对于一个区间 ，如果存在区间 满足 且 ， 则这等价于 且 。这还意味着 是唯一的满足 的区间 。
我们称 是 的关键区间。
考虑一个大于两个集合构成的等价类 。我们 钦定 。容易发现这种情况只会发生在 时。发现对于相交的 与 （）， 当且仅当 是 的关键区间。
我们希望对于 只减去 的贡献方便统计。考虑如下算法：先默认答案为 ，枚举 ，增加 ，如果存在 且 ，则将 答案减一；如果 对于这个 首次出现，则将答案额外减一。容易发现上述 算法的正确性。直接实现复杂度小常数 。
尝试加速统计。从右到左扫描 ，对于每个 ，维护 表示 和 。这可以通过一个经典的单调栈技巧实现（通过单调栈将 操作转为区间加减）。
需要统计所有 的位置以及满足 的位置中 出现的种数。由于 ，所以统计 的个数只需要记录 的最小值以及最小值的个数。由于 不增，种数即为颜色段数。这些信息都是容易合并的，直接用线段树维护即可，复杂度 。
模拟赛题解/2025.10.10 模拟赛
· 阅读需 9 分钟
T1-我来，我见，我征服（cerydra）
题面
「凯撒」刻律德菈新发明了『征服棋』，这与国际象棋完全不同。
棋子，表示棋盘上的领土，都是长宽均为整数，且长宽比为 的长方形。棋子数量充足，你可以认为每种大小的棋子都有 个。
第一次落子可以选择一枚任意大小的棋子，表示初始的领土；接下来每次落子都是 领土扩张。落子需要满足如下条件：
- 不能与之前的棋子重叠；
- 必须有一条边与之前的领土相邻；
- 落子后，领土必须仍为矩形，但长宽比可以不是 。
「凯撒」刻律德菈最忠诚的剑旗，海瑟音问你：至少和至多分别要落多少棋子，领土形状才会成为 。 数据保证存在至少一种落子方式，使得领土形状都为 。
。
题解
我们先考虑不带任何优化的搜索且 ：
- 对于 我们直接全删掉。
- 对于 是偶数，我们显而易见可以删掉 的一个矩形。
- 对于 可以删掉一个 的一个矩形。
- 对于 可以删掉一个 的一个矩形。
然后我们考虑记忆化搜索，再考虑优化：
- 我们发现对于 时，我们设 可以一次性删除 个 的矩形，将 减小到 。
T2-让告别，更美一些（castorice）
题面
安眠地的花丛中，有 朵盛开的安提灵，第 朵安提灵的高度是 。
遐蝶已经将安提灵的高度修剪得互不相同，换而言之， 是一个长为 的排列。
她将进行若干次操作以把数列 变成目标数列 。一次操作为选择 ，交换 中的最大值和最小值。例如，如果 为 ，操作 会使得 变成 。
遐蝶邀请你一起修剪花丛，你需要找出一种将数列 变成数列 的操作序列。
如果有多种可能的操作序列，你可以输出任意一种。
你需要保证操作序列长度不超过 。
。
题解
注意到操作可逆，结合特殊性质 B 的提示想到可以将 分别排序，再翻转操作序列。
考虑分治进行排序，合并两个有序的序列时：
- 如果它们值域上不相交，先将它们分别翻转，变成下降序列，然后翻转回来。需要使用 次操作。
- 否则对值域分治，如下图选择中位数将两个序列分开，对中间部分应用上述方法排序，得到两个子问题，递归即可。
时间复杂度类似 CDQ 分治， 可以通过。
T3-因你而在的故事（cyrene）
题面
昔涟给你讲了一个不同以往的浪漫故事：很久很久以前，有一个整数 和守护这个数的昔涟（迷迷形态）。
你可以询问迷迷一个整数 ，如果 ，迷迷会回答“”；反之，回答“”。
为了猜出 ，你想到了以下策略：先创建一个长为 的排列 ，然后按 到 的顺序依次猜数。
你会跳过不必要的猜测：如果你已经猜过 ，迷迷回答“”而你现在要猜 ，则你跳过这次猜测；对称地，如果你已经猜过 ，迷迷回答“”而你现在要猜 ，则你也跳过这次猜测。可以说明，对于任意一个排列，该策略都能够猜出 。
你想统计对于所有排列 ，你能让迷迷在连续两次询问中，发出的声音拼接后为“\text{Me}\!\!\nearrow$$\text{Me}\!\!\searrow”的次数的总和。
昔涟当然发现了你在占她便宜，她也发现答案可能很大，所以抓住你的手在题目描 述最后写下：答案对 取模。
。
题解
或 时答案为 。
当 时，记 ，结论：
规定 ，则 时上式正确。
只需要归纳证明： 不变， 变成 ，即向原排列插入 （回答“”）时，期望的变化量
如果 插入在此前第一个回答“”的数之后，它会被忽略。所有未被忽略的回答“”的数将排列分为 段，因此此前第一个回答“”的数之前的数的个数的期望为 。
- 只要 插入到下标在 中的值最大的数之前就会与一个不被忽略的“”拼出一个 贡献，所以 产生贡献的期望为 ；
- 上述期望需要减掉排列的第一个数对应的回答是“”，即上述最大值不存在时多算的期望 ；
- 两项加起来与需要证明的值相等，于是证明该结论正确。
该式可以 预处理， 计算。
T4-哀丽秘榭（phainon）
题面
哀丽秘榭有 块沿水渠分布的麦田，你可以将麦田视为一棵无根树。
经过多年的积累，哀丽秘榭培育出了 种优质小麦品种，第 块麦田种植第 种小麦，每一种小麦都有至少一块田在种植。
白厄从神悟树庭带来了每种小麦对应的肥料，他需要对于每种小麦，指定恰好一块种植了该种小麦的麦田，将肥料堆放在这里。记第 种小麦堆放的麦田编号为 。
为了不在施肥时出错，白厄希望对于每块麦田 ，满足 ，其中 表示麦田 和麦田 之间水渠的条数。换而言之，麦田到其所属集合中有小孩的麦田的树上距离必须小于到其它任何集合中有小孩的麦田的树上距离。
白厄找到你，请你构造一个合法的 ，或者说明无解。如果你能正确判断是否有解但有解时你不会构造 ，你也可以得到部分分数。
如果有多种可能的 ，你可以输出任意一种。
子任务的得分为其包含的各测试点的得分的最小值。对于单个测试点：
- 如果你不能正确判断是否有解，或者输出格式错误，获得 的分数；
- 如果能正确判断是否有解，但是有解时构造的 不合法，获得 的分数；
- 如果能正确判断是否有解，并且有解时构造的 合法，获得 的分数；
。
题解
一组解 是合法的，当且仅当：
- 相同的点连通；
- 将 相同的点视为一个连通块，相邻两个连通块的 到连接这两个连通块的边的距离相等。
先判掉 相同的点不连通的情况。
设 表示处理 所在的连通块的子树后， 能否堆放肥料。连通块 的限制为：
- 设与其相邻的连通块 中 的节点 到连通块 边界的距离为 ，那么 到 边界的距离也为 ；
- 满足来自 的所有 给出的限制中的任意一个即可。
这可以转化为设 边界的边偏向 一侧的点为 ，连通块 中到 的距离在一个集合（这个集合由连通块 中的点 给出）中的点全部加一，最终被加的次数等于与 相邻的连通块数的点令 ，否则 。
使用点分治完成上述处理即可判定是否有解，构造时按 数组依次推导即可，时间复杂度 。
模拟赛题解/2025.10.8 模拟赛
· 阅读需 5 分钟
T1-加法问题（at）
题面
给定 个正整数 。
乐嘉维林要计算这 个数的和，他会先创造一个数 初始是 ，然后他会从左往右依次将 加上这个数。
加法是很困难的操作，进位往往是加法中的难点，因此，乐嘉维林希望十进制下进位次数最少（如 会产生一次进位）。
请你将序列 重排使得乐嘉维林计算过程中进位次数最少，你只需要输出这个次数。
。
题解
注意到，只改变顺序而不改变数值的情况下，十进制每一位产生的进位数量是不变的，因此直接模拟进位加和即可。
复杂度 。
T2-树上问题（tp）
题面
给定一个 个点的树，点有颜色，问有哪些 满足，对于任意的 ，路径 上不出现重复颜色。
。
题解
我们从一个颜色出现次数不超过 入手，此时我们发现限制相当于答案必须在某个子树内/外，直接用 dfs 序列维护即可。
如果 是同一个颜色，我们直接考虑 这些二元链产生的限制，那么我们实际上忽略了三元链的情况，然而三元链本身不可能存在解，因此我们只要将满足如上限制得到的答案中的任意一个校验一下即可。
T3-排列计数（cp）
题面
给出三个正整数 和 。
有多少个 的排列构成的有序 元组，，满足：
- 字典序：。
- 逆序对数：。
设 为答案模 的值。对于所有 ，请你输出 。
。
题解
我们定义 为长度为 的排列按照字典序排列之后逆序对数量得到的序列。
那么这个题就是要求 中长度为 的下降子序列。
我们发现 是由 全体加 ，加 ，，到加 得到的序列。
那么我们定义 为 中选出长度为 开头为 结尾为 的序列的方案数，那么转移的时候每次 变成 中每一段内部 值除了 产生了部分平移之外都相同， 的合并直接做类似矩阵乘法和卷积的合并即可。
时间复杂度为 。
T4-剧镇计算（mc）
题面
给定一个整数 ，以及一个 的矩阵，每个格子中写有一个数，格子 初始写着 。
给定 个二元组 。
你可以进行如下操作：选择任意 满足 ，任意非负整数 ，对于每个 从 到 ，将 位置的数替换为 （这里 表示异或操作）。
你的目标是使所有格子中的数都变为 ，请输出最小操作次数。
可以证明一定有解。
题解
本题难度极大，选手可以尝试完成一些部分分。
最基础的观察是，如果我们发现一个我们不会对同一个 操作 次，因为如果操作了 和 ，那么我们不如直接操作 。 接着我们可以发现操作方案本质上是唯一的，所以说我们定义矩阵乘法 时 ，那么这个问题本质上就是给定两个矩阵 ，我们要得 到一个矩阵 ，满足 。
特殊性质A
我们直接尝试求出 矩阵的逆矩阵，由于 矩阵仅有一行，所以其逆矩阵一定也可以只有一行，直接高斯消元即可。
特殊性质B
我们发现对于矩阵 ， 等价于 中 点的值转移到位置 （因为其他点位都会被抵消， 与 会转移到同一个位置）。
所以说 实际上就是一个左上角是 其他位置是 的矩阵。 也就是说 是原矩阵 T 的逆元，所以我们直接计算 即可。
时间复杂度 。
模拟赛题解/2025.10.7 模拟赛
· 阅读需 9 分钟
T1-分组（group）
题面
麦克班上一共有 个同学（不包括麦克，麦克作为班长，需要将所有同学（除自己以外）划分为若干个小组，以方便管理。
为了让大家尽量满意分组的结果，麦克用独立程度来描述每一个同学，即其希望自己所在小组的人数 独立程度。
经过观察，麦克得到了每个同学的独立程度，其中第 个同学为 。
麦克很快分好了组，但他并不满足于此，他希望求出一共有多少种本质不同的分组方式。
这里两组方案本质不同当且仅当存在两个同学，其中一组方案中两人在同一组，而另一种方案中两人不在同一组。
由于答案可能非常大，只需要求出对 取模后的结果。
提示：每个同学需恰在某一组中，且每组均需至少包含一个人。
。
题解
定义 表示确定了人数 的组且有 个 的人加入，设有 个 和 个 ， 转移即
根据调和级数，时间复杂度为 。
T2-奇迹（miracle）
题面
阿尔瓦·洛伦兹正在进行着新一轮的电学实验。
他有 块质地相同的金属，每块金属已经均匀带上了一定的电荷，电荷量可以是任意实数，初始时，每块金属的比荷都是整数。
阿尔瓦希望通过一些操作使得这 块金属的质量和电荷量达到自己的预期，但是他不知道这是否可能实现，于是请你帮助他验证一下。
初始时，第 块金属的质量是 ，比荷是 。阿尔瓦希望通过操作使得第 块金属的质量仍为 ，比荷为 。
阿尔瓦的操作分为以下两种：
- 将一块金属分割为两部分，使得两部分的质量和等于原来金属的质量；
- 拿起两块金属（不要求相邻）让它们融合，新合成的金属的质量和电荷量是原来两块金属对应物理量的加和。注意比荷不一定是加和，需要重新计算。
你可以认为金属质量和电荷量足够大，是可以被无限分割的，且分割后仍保持均匀带电状态，分成的两部分的比荷不变。
操作可以进行任意次。你需要判断是否存在一种方案使得目标被达成。
。
题解
想象这样一个场景：你手头有一张借记卡（不能欠款），你会不停地收入一些钱，花掉一些钱，当一次消费的金额大于卡内余额的时候，这次消费就不能进行了。
到这个题里，我们也可以开一张「能量借记卡」。
我们将本题的一些概念用金融中的术语表达： 可以认为是第 笔账单的数量， 可以认为是每笔账单的支出（因此初态中的第 个杯子可以变成 个单价为 的商品）；同理， 可以认为是每笔账单的收入（因此终态中的第 个杯子可以变成 张每张票面金额为 的支票）。
首先将初始状态的 个杯子按温度升序排序，终态的 个杯子也按温度升序排序。
接下来我们搞两个指针 ,，刚开始 指向初始态的第一个杯子， 指向终态的第一个杯子。
我们现在可以用 中的支票去买 中的商品。当然商家很刁钻，一张支票只能买一个商品。
如果一张支票的金额大于一个商品的钱，我们就可以将多余的钱（或者说是能量）存进银行卡，如果一张支票的金额小于一个商品的钱，我们就需要从银行卡里取些钱（能量）了。
（ 中的商品数和 中的支票数可能不一定相等，不过这不是问题， 空的时候就将 向后移动， 空的时候也将 向后移动就行了，别忘了总商品数和总支票数是相等的）
因为我们手里拿的是借记卡，所以任何时候余额都不能为负。
如果我们顺利地走完了上面的整个过程（也就是说没有赊账的情况发生），说明有解。否则无解。
T3-渔猎（fishing）
题面
格蕾丝让杰弗里·博纳维塔给自己创造了一块大小为 ，且左右边界、上下边界连通的区域，然后在这个区域里围出了 个矩形的闭合水渊。
现在，记忆只有 7 秒钟的格蕾丝有点分不清每个水渊的范围了。她只记得每个水渊 矩形的两个对角顶点。格蕾丝发现，只知道两个对角顶点的情况下每个矩形的可能情况 有不止一种。她想问问你在最好的情况下，同时被n 个水渊包围的面积最大是多少？
。
题解
横纵坐标是独立的。
我们发现一对顶点的作用是把 和 坐标划分成了两个部分，使得这两个部分不可能同时被覆盖到，且具体覆盖到哪个区域我们可以自己指定。于是开线段树，对值域进行哈希。以 坐标为例，若两个顶点的 坐标分别是 ，则可知 和 必然不可能同时被覆盖，我们需要给它们不同的哈希值。
最后哈希值相同的部分大概率能被一起覆盖，那么分别取 坐标里出现次数最多的哈希值，乘起来就行了。
这个大概率是多大呢？如果你用 位随机数，这个概率确实不够大，用 位随机数就可以了。
T4-影袭（strike）
题面
看到格蕾丝练习洄游，桑格莉娅也想练习一下自己的表演能力。
桑格莉娅准备了一块大小为 的空地作为训练场地。
桑格莉娅的一次歌剧表演从左上角 开始，经过若干次距离为 的移动后，到右下角 结束。由于对于效率比较注重，桑格莉娅只会向右或者向下移动。她不能移动到障碍上。
初始时，训练场地是空的。鉴于在空舞台上表演有点简单，桑格莉娅决定给自己上上难度。她准备了 次操作，每次操作形如“ 在 位置摆放一个障碍 ”，但她发现有些障碍的摆放可能使得自己接下来无法表演，因此她只会在障碍摆放完后仍然可以进行表演的情况下摆放障碍。对于每次操作，她想知道这次操作是否会因为影响表演而被忽略。
桑格莉娅想和你一起讨论障碍的布置方式，因此这些操作的给出都是在线的，你需 要在她给出一个操作后立刻回答。
。
题解
贴模型走路是一个很实用的技巧，可以在这类网格路径题中有效地去除一些重复冗余状态。
比如这道题，定义首末两行、两列为边缘部分，其他为非边缘部分，我们可以发现无论怎么在非边缘部分添加障碍，都存在至少两条合法路径，如下图：
ooooo
o.x.o
oxx.o
ox.xo
ooooo
X 表示障碍，O 表示边缘部分，. 是普通的空地。我们发现只要存在边缘部分，我们就不用管普通的空地。
但是边缘部分可能会改变。比如在一个空的 网格中添加一个障碍：
ooox.
o.ooo
o...o
o...o
ooooo
不难发现障碍的作用是“如果处在原来的边缘部分，就把这个边缘部分挪个地方到左下角/右上角”，或者说“如果处在原来的边缘部分，则令自己左下角/右上角不可能再为边缘部分”。到底哪个角就要看自己原先处在左下角的边缘还是右上角的边缘。如果同时处在两类边缘，那说明没有路径可以走了，此时输出 Yes，我们也顺便获得了是否有路径的充要条件。
边缘的修改是可以均摊的，因为每个点最多被一类边缘用一次，于是写一个事件驱动模拟。其中需要找最大最小值，set 常数大，换成懒惰删除的堆就可以了。
题解：P11109 [ROI 2023] 会议 (Day 2)
· 阅读需 2 分钟
原题链接
题意简述
有 个区间（ 是偶数），要求选出 个区间，满足其最小点覆盖刚好是原先 个区间最小点覆盖的一半（满足原先 个区间最小点覆盖也是偶数）。
解题思路
妙妙题。
首先考虑我们该如何选择区间，经典对区间右端点排序并贪心选择。
注意到在选区间的过程中，两两被选择的区间 之间，编号为 的区间只要 被选择了，一定不会被选择。
因此我们只要在初始的 个区间中选出 个作为最后被选的区间，这 个区间各自的后继一定数量的区间一定可以被选中为 个区间之一并不影响最终选择的区间。
由于我们要取的是 个，因此这 个区间中一定有 个区间满足后继可扩展的区间数量之和 。
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 100005;
int T , n , nxt[N];
vector <int> v , ans;
struct point{int l , r , id;} p[N];
signed main()
{
cin.tie(nullptr)->sync_with_stdio(false);
cin >> T;
while(T--)
{
cin >> n;
for(int i = 1 ; i <= n ; i++) cin >> p[i].l >> p[i].r , p[i].id = i;
sort(p + 1 , p + n + 1 , [](point x , point y){return x.r < y.r;});
int lst = 0; v.clear();
for(int i = 1 ; i <= n ; i++) if(p[lst].r < p[i].l)
{
if(lst) nxt[lst] = i;
v.emplace_back(i) , lst = i;
}
nxt[lst] = n + 1; ans.clear();
// for(auto x : v) cout << x << ' '; cout << '\n';
sort(v.begin() , v.end() , [](int x , int y){return nxt[x] - x > nxt[y] - y;});
for(int i = 0 ; i < v.size() >> 1 ; i++) ans.emplace_back(v[i]);
for(int i = 0 ; i < v.size() >> 1 ; i++)
{
if(ans.size() == n >> 1) break;
for(int j = v[i] + 1 ; j < nxt[v[i]] ; j++)
{
ans.emplace_back(j);
if(ans.size() == n >> 1) break;
}
}
for(auto x : ans) cout << p[x].id << ' '; cout << '\n';
}
return 0;
}
模拟赛题解/2025.10.6 模拟赛
· 阅读需 5 分钟
T1-开端（bgning）
题面
给定一个长度为 的非负整数序列 以及两个正整数 和 。
一次操作定义为交换序列 中任意两个相邻元素 和 。
求最少的操作次数，使得操作后的序列 满足 。
。
题解
设 表示在选了 个数，下标和为 的最大和。
于是问题就转化为一个类似背包的问题，最后只需要计算最小的 使得 即可，操作次数即为 。
直接 解决。
T2-发展（dvlpmnt）
题面
给定一个长度为 的序列 ，你需要从中选出一个元素个数不小于 的子序列，使得这个子序列中所有元素的 最大。
你只需要求出这个最大值即可。
。
题解
注意到，因为最终的 是至少 个数的因数，所以可以考虑直接随机选择一个数。
随机选择 次之后，选不到任何一个最终答案的倍数的概率为 ，几乎可以忽略。
于是直接 枚举所有当前数的因数，并且 找到所有数和当前数的 。
最后 得到所有因数的出现次数（其中 为当前数因数个数），从大到小枚举得到的第一个 的值对答案进行一次更新。
复杂度 。
T3-高潮（climax）
题面
给定一个 行 列的棋盘。每个格点被染成红色（R）或蓝色（B），其中红色格点和蓝色格点各占一半，即各有 个。
保证棋盘的左上角格点 为红色，右下角格点 为蓝色。
将所有红色格点之间两两连边，所有蓝色格点之间两两连边。
你需要判断能否将这些边定向，使得定向后的所有 个有向量之和为 。
请输出任意一种构造方案。如果无解，则输出最小的偶数 ，满足 不能被表示为两个素数之和。
。
题解
注意到，当 为奇数的时候，每个点的度数都为偶数，可以直接欧拉回路解决。
当 为偶数的时候，每个点的度数为奇数，考虑直接先不去除掉 和 ，按照 为奇数的情况处理。
最后可以发现，只要从 向所有红色点定向，从 向所有蓝色点定向即可，可以证明向量和一定为 。
复杂度 。
T4-结局（cnclusn）
题面
给定两个非负整数 满足 。
对于一个长度为 的整数序列 ，满足 且 互不相同，我们按如下规则定义 ：
- 将 按照从小到大的顺序排序；
- 将序列进行一次差分，记 为差分后的序列 ；
- 将 按照从小到大的顺序排序；
- 将 进行一次前缀和，记 为取前缀和后的序列 ；
- 定义 。
记 为当序列 在所有 个满足长度为 且 且 互不相同的序列中均匀随机选取时 的期望值（即 的第 个元素的期望值），你需要对于 求出 ，输出实数结果。
。
题解
设 表示如果选择 个数，且每个数不超过 的前提下， 的期望是多少。
显然，我们需要要求的即为 。
不妨设差分序列内严格大于 的元素有 个，这种情况出现的概率为 。 则对 ，我们有转移：
- 。
由于本题要求输出实数，因此实现时需要注意精度问题。例如在计算组合数时，应使用递推方式 来避免精度误差。
复杂度 。
模拟赛题解/2025.10.5 模拟赛
· 阅读需 8 分钟
T1-诋毁原神（slander）
题面
在提瓦特大陆上存在着 种元素，刚刚来到这片大陆的旅行者对第 种元素掌控力 。
但是这样的成长速度还是太慢了，因此旅行者为了快速提升自己各种元素掌控力接受了 场测试。
具体的，每一场测试 都会考核所有 种元素掌控力，若此时旅行者对于所有元素 的掌控力 均 ，那么旅行者将通过这场考验，并且第 种元素掌控力将提升 ，即将 加上 。
旅行者可以以任意顺序参加测试，但每一场测试只能参加一次。同时，她希望尽可能多的提升自己的实力，请你帮助她计算出最多能通过的测试数量。
，，。
题解
考虑一个显然的贪心：每次选择所有能通过的测试中，提升向量 的“综合提升”最大的那一个。
然而这在多维情况下未必正确。
可以将这个问题看作多维偏序：每个测试 有要求向量 ，收益向量 。
若旅行者当前掌控力向量为 ，则可以选择所有满足 （按分量）的测试，并使 。
这其实是一个「多维可达性问题」，但维数可能较大。
注意到 ，可在所有测试之间建立依赖关系图：
若 ，则 需要在 之前完成。这样得到一个 DAG。
于是问题转化为： 求该 DAG 的最长路径长度。
复杂度 建边后 拓扑 DP 即可。
T2-理解原神（realize）
题面
在提瓦特大陆上有 个城市，这些城市由 条长度为 的无向道路相连，并且可以从任何一个城市走到任何另一个城市。
旅行者在这 个城市中选择了一个城市进行休息，然后规划接下来的行程。为了方便，她记录下了各个城市 到她选择休息的城市的最短路长度，记作 。
可是她已经忘记了某一些 ，也可能记错一些 ，也忘记了她选择休息的城市，请你帮助旅行者确定她选择的城市可能是哪些。
，，，并且保证图没有重边自环。
题解
我们要判断哪些点 可以作为起点，使得与已知 一致。
一个朴素想法是：枚举 ，从 BFS 得到最短路，与给定的 对比。
显然复杂度 不可行。
可以反过来思考：
若某个点 被确定距离为 ，则所有相邻点 必然满足 。
若某个 ，则它对结果没有约束。
我们可以把所有有已知 的点作为锚点，检查其相邻点的约束是否矛盾。
更高效的方法：
以所有 的点为可能的根，从这些点 BFS；
若能得到一个与已知 一致的距离分配，则该根可行。
由于每次 BFS 复杂度 ，而起点数量可能较多，
可以预处理一遍全局距离：对所有已知 建立一个「多源 BFS」即可同时验证所有可能的根。
整体复杂度 。
T3-追随原神（follow）
题面
旅行者正在为其他冒险者设计一个秘境！
旅行者决定在一棵由 个节点、 条边构成的树上建造这个秘境，1 号节点为这棵树的根节点。定义 表示 节点的父亲节点，每条边 上都标有符号 和 。
她有 个宝箱，价值分别为 ，她希望将这些宝箱放置在每一个节点，记节点 上放置宝箱的价值为 ，则需要满足：
- 对于标有 的边 ，需满足 。
- 对于标有 的边 ，需满足 。
请你帮助旅行者计算她有多少种放置宝箱的方案数，这个结果可能很大，只需输出对 取模的结果。
，并且 有 。
题解
考虑一棵树，每条边 带有方向约束：
若为 ，则 ；
若为 ，则 。
我们要计算所有合法赋值 为 的排列的数量。
显然这是一个偏序计数问题。
树形偏序的拓扑序数量可通过 DP 求得。
设 表示在子树 内有 个元素时的方案数。
子节点之间根据符号 或 决定合并时的排列组合数。
合并两子树的转移可用组合数：
由于 ，可用树形 DP + 前缀卷积实现，复杂度 。
实现上先对所有子树求大小和 ，然后自底向上合并。
最终答案为 对 取模。
T4-成为原神（become）
题面
在提瓦特大陆上，有 个城市，它们由 条可以相互到达的道路连接起来，为了交通的便利，每一个城市都能通过若干条道路到达任意其它城市。
旅行者对于一条道路是否有挑战有着独特的看法，她为每一条道路 设置了一个评分 ，同时她认为一条路径的难度为路径上经过道路的最大评分与最小评分之和。旅行者现在在城市 1，为了确定下一步的行程，希望你能帮助她对于每一个城市 计算出所有 （不重复经过同一条道路）的路径难度的最小值。
，，对于每一条道路 都有 ，。
题解
对于 Subtask 2，本质是确定了最小值，要使 路径上边权取最大值最小，显然直接上 Kruskal 重构树。
对于 Subtask 3，本质是确定了最大值，要使 路径上边权取最小值最大，显然直接跑边双即可。
这启发我们考虑枚举一条边，让它成为最大值/最小值，容易发现枚举最大值是更有前途的。
将所有边按边权从小到大排序，依次枚举一条边，这条边就是当前的最大值，现在可能经过这条边之前的边。
同时注意到一条边如果在 的路径上，那么也一定在缩完边双后的 的路径上。那么考虑加入一条连接 的边带来的影响：
- 若 已经在一个边双里面了，则没有任何影响，因为这条边一定比已经在边双中的所有边都大。
- 若 已经在同一棵树，但不在同一个边双内，则需要把 路径上所有点缩起来，这个点的点权是路径上所有点权和边权的最小值，然后更新子树内所有点的答案。
- 若 不在同一个连通块内，直接把 连起来即可。
直接暴力处理这三种情况，复杂度是 的，考虑优化。
注意到第三种情况边一定是最小生成树上的边，于是先跑出整个图的最小生成树，预处理到每一个点的点权。
现在的问题是，某个点可能在还未与 连通的时候就记录了答案，因此我们需要在每个点与 所在连通块连接时，重新计算这个点的答案。
用两棵线段树，分别维护树上路径的最小值和实际的答案，需要支持区间 check min，单点修改和单点查询。
对于第二种情况的缩点操作可以用并查集维护，让并查集的树为连通块深度最小的点即可，复杂度是均摊的，总复杂度 。
模拟赛题解/2025.9.30 模拟赛
· 阅读需 8 分钟
T1-序列（array）
题面
有一个长度为 的正整数序列 ，其中 在 范围内等概率随机生成。
这样序列的总情况数就是 。
对于一个生成出的序列 ，设 ，该序列的权值为 。
求全部 种情况生成的序列的权值之和，对 取模。
。
题解
枚举 ，统计贡献，此时数列每一项都必须 ，每一项的 是个连续段，简单等差数列求和，然后把每一项的和乘起来。
但是这里会误算一些贡献，误算的是所有项都没取到 的，也就是所有项都 的，这样的情况每一项取法也是个连续段，所以也是等差数列求和后乘起来（注意计算这个结果时序列最大值还是按 计算，这样一减就是把误算的都删了）。
也可以设 表示考虑了前 项，是否有至少一项取到了 的结果， 转移。
最终时间复杂度均为 ，其中 表示值域。
T2-账本（book）
题面
一个长度为 的记账单， 表示存入 元钱， 表示取出 元钱。初始时账户上有 元钱，最终账户上恰好有 元钱。
现在发现记账单有问题，你要把记账单修改正确，使得：
- 账户上的钱数永远非负；
- 最后账户上恰好有 元钱。
你可以进行任意次操作，每次操作可选以下两种之一：
- 对某一位取反，耗时 ；
- 将记账单循环右移一位，耗时 。
求最小总耗时。
。
题解
算法1
注意到操作 和操作 的顺序不影响答案，于是可以 枚举对哪些位置进行操作 ，再 枚举进行多少次操作 ，最后 检查该方案是否合法并更新答案。 时间复杂度为 。
算法2
先枚举操作 的次数 ，下面考虑贪心地进行操作 。
记原来的账本为 ，其中 对应 ， 对应 。
那么进行了 次操作 后得到的账本是 。
求出账本的前缀和 。
为保证修改后任意一个前缀和非负，只需保证当前的最小前缀和在修改后非负，如果当前的最小前缀和是负数，则先将该前缀中最前的一定数量的 改为 ，计算出这种操作的次数，并记录对 的影响。
再调整 次，使账本满足结束时是 元的要求。
时间复杂度 。
算法3
注意到操作的代价可以 计算，时间瓶颈在于找到前缀和最小的位置。
为方便可以将 复制一遍接在后面得到一条长为 的链 。
对扩展后的数组求前缀和 ，则进行 次操作 时前缀和最小的位置即为 在区间 上的最小值的位置。
因为 的左右端点都是随 单调递增的，所以可以用单调队列求出最小值的位置。
也可以看成每次取原数组 的一个后缀拼上一个前缀，设 的前缀和数组为 ，那么我们想要的最小值就是 的后缀最小值或者 加 的前缀最小值里。
时间复杂度 。
T3-删数（delete）
题面
介绍一种删数游戏。
对于一个数组 ，每次操作他需要找到一个数 ，满足此时数组的第 个数正好是 ，然后删除这个数，后边的数依次向前补位。如果此时有多个 满足条件，小 A 可以自主决定本次操作删哪个数。
小 A 想知道在最优策略下，他最多可以删除多少个数？
为了增加难度，小 A 会进行 次询问，每次询问给定两个数 ，询问的是将 和 全部临时改为 后，对 数组进行删数游戏，最多可以删除多少个数。
询问之间互相独立。
。
题解
算法1
有能删的数的时候一定删除最后边的，这样不会让前边本来能删的变成不能删，模拟时间复杂度不超过 。
算法2
对于 的问题，我们枚举 从 ，如果新添加的 且 ，那么在操作的过程中一定有某一时刻能删除 且不影响其它任何数，所以 就加 。
这个做法同时能以 的时间复杂度过掉 的测试点。
算法3
枚举 从 ，可以发现 越小，能删除的一定越多，用一个数据结构维护 取每一个地方的时候的答案，可以发现当 从 变到 的时候是该数据结构上一个前缀加 。
每次我们就线段树二分找到 的最后位置 ，然后对 区间加 。
时间复杂度 。
T4-选数（select）
题面
从正整数 中选出若干数满足以下条件：
- 如果 被选中，则 都不能被选中。
问有多少种不同的选数方法（什么都不选也算一种满足条件的选法）。
两种方法不同当且仅当至少存在一个数在一个方法中被选中而在另一个方法中没有被选中。
答案对 取模。
。
题解
一个数 可以写成 的形式。
对于每个 （ 中不含质因子 ），构造一个二维数组，把 写在左上角，同一行从左往右乘 递推，同列从上往下乘 递推，超过 的就不能选。
问题转换为求选择不相邻的若干数的方案数，因为行列数都是 级别，所以可以状压 。
用轮廓线 的方法进行状态 复杂度会较低，设 表示依次考虑每个格，考虑完 这个格以后第 行一个截止到 的前缀拼上第 行一个从 开始的后缀的状态为 的答案。
枚举下一个格选还是不选进行转移。
应该可以直接过起码 50 分。
考虑优化，可以发现把 写在左上角，把 作为大小限制，其实跟把 写在左上角，把 作为大小限制是一样的。
因此可以使用数论分块优化枚举 的过程。
进一步，如果这次的大小限制算出的有效行数和每一行的有效列数都和上一次一样的话，可以不重新推，直接用上一次的结果即可。
另外 的状态数也可以优化，可以发现有效状态中最多有 处相邻的 （出现在第 行和第 行拼接的那个地方），只保留这些状态进行 。
把这些优化都做了就可以通过 的数据了。
模拟赛题解/2025.9.29 模拟赛
· 阅读需 6 分钟
T1-墙壁（wall）
题面
一个长为 的排列 ， 被称为墙壁点，当且仅当满足 且 可以作为一个非退化三角形的三边的长度。 组数据，每组数据给出 ，构造一个长为 的排列，恰有 个墙壁点。
。
题解
首先构造无解当且仅当 ，尝试考虑 的情况。
若要构造使每三个数都不满足条件，则可以尝试将每 个数分开，然后三个分为一组。
则任意两数和一定可以构造为小于第三个数，考虑构造为对于每三个，大段和中段放最大的，小段放最小的，显然一定可行。
单次复杂度 ，总复杂度 。
T2-众数（wsx）
题面
给定一个整数 ，初始排列为 ，即 （）。 你需要处理 个操作，操作有两种类型：
- ：查询区间 上所有元素的和。
- ：将当前排列替换为它的下一个排列，重复 次。例如，如果 且当前 排列为 ，则执行如下变化链 。
。
题解
注意到实际上 的改变范围使得只有最后 位可能被改变。
直接暴力康托展开/逆康托展开，维护最后 个元素即可。
复杂度 ，常数较大，但是时间充裕。
T3-蹭网（network）
题面
在一条高速上有 个城市。第 个城市安装了一个功率为 的天线，使其网络覆盖从 到 的所有城市。
一些大运会沿着这条路从城市 移动到城市 ，其中 。大运在经过的每个城市都会蹭覆盖该城市的某个网络。
因为更换蹭的网容易被网络管理发现，因此大运司机们切换网络的次数会尽可能少。用 表示从城市 到城市 的大运在途中蹭的网络改变次数（）。初始在城市 蹭的网不算作改变次数。
定义蹭网危险度 为 的总和，即：
现在大运司机们众筹了一个新天线，功率为 。为了降低蹭网危险度，可以用新天线替换任意一个现有天线。你需要确定，如果最多替换一个天线为功率 的新天线，危险度 最小可能是多少。
。
题解
首先考虑求出不更换天线时的 。显然最优策略是在换网时选择覆盖当前点的天线中 最大的蹭，并一直使用该网直至 。发现该形式可以简单用 刻画。
记 表示从城 开始走到城 的代价之和， 表示覆盖城 的天线中最大的 。则：。记此时不带修改的 为 。
现在需要对于每个 计算将 替换成 后的代价。注意到在仍保留天线 的选择下，若 则不会改变 ，否则与 不存在的情况等价。因此可以不用去除 的影响，直接考虑加入 的影响。
（下记 对应的 为 ）
记 表示覆盖城 天线中最小的 。则加入 相当于使在区间 中的 的 变成 。
记经过上述区间的大运有 辆，其原本贡献为 ，则新答案为：。
从左往右处理 ，记 表示从 出发到 的点数，转移为：。
则 相当于区间内 的和， 相当于区间内 的和。
从左到右扫描线，由于 递增，边界只会改变 次，可以用 BIT 处理边界变化产生的贡献。
复杂度 。
T4-冰霜行者（frost）
题面
大湖是一个完美的巨大的圆。圆上等距的分布着 个港口，顺时针编号 到 ，但是水里和外面的陆地有十分危险的存在，所以最开始港口间两两独立，互不可达。房主决定用冰霜行者在港口间直直地走出冰道。由于大湖真的很大，港口可以看作点，冰道可以看作线段。
依次发生 个事件，每个事件形式如下：
- 表示房主在 号港口间使用冰霜行者建造一条冰道；
- 表示询问 号港口和 号港口间是否可达。
单步可达的定义：连接了某个港口的冰道与该港口单步可达；任意位置相交的冰道间单步可达。单步可达关系是双向的。
可达的定义：可通过若干次单步可达走到。可以证明，可达关系是双向的，且有传递性。
。
题解
注意到有效合并总共只有最多 次，每次和之前所有边查一下哪些有交，再和端点合并。
首先断环成链，对于每个连通块只保留相邻链和最外层一条边。
根据题目性质，不同连通块间不可能有边相交，所以任意两个连通块要不然相离，要不然一个被夹在另一个的相邻两点间。
于是合并两个连通块只需要修改 条边。连通性仍然直接拿并查集维护。
现在的核心问题是怎么加新边：使用线段树维护每个点被边覆盖了几层，设其为 。合并 时如果穿过了某条边，那么一定穿过了 间某个 的点连出去的边。
找到 右边第一个这样的 ，直接把它和 各自所在连通块合并，然后重新试图合并新连通块最右端点和 即可。
复杂度 。
模拟赛题解/2025.9.27 模拟赛
· 阅读需 6 分钟
T1-路径（path）
题面
现有一张 个点、 条边的无向连通图，图中没有重边和自环，点和边都从 开始标号。初始时，小 在图中结点 的位置上。
小 A 想要在图中游走，但他的行动受到一定的限制。具体而言，我们定义他的“一步”移动过程如下：
- 选择他当前所在点的一条邻边，并移动到该边的另外一个点。
- 他可以选择是否删除他刚才选择的边。如果他选择删除该边，那么他之后无法再次经过这条边；如果他选择保留该边，那么这一步移动对他之后的行动没有影响。
小 希望最后恰好剩下 条边，并且这些边构成一棵树。但由于小 A 非常懒，因此他又希望他的移动不超过 步。
请你为他构造一条满足上述要求的路径。数据保证一定有解。
。
题解
首先考虑一条路径的代价：设路径长为 ，则代价为 。注意每个点只会被算一次。
考虑 DP，设 表示从 到 的路径代价的最大值。转移就是 。
由于是树，转移可以做，但复杂度太高。
考虑换根：树形 DP。设 表示以 为根子树中，经过 的路径最大值。则 。
然后 DFS 两遍即可得到全局最优解。
复杂度 。
T2-命题（proposition）
题面
小 有 个命题，这些命题按某种顺序从 到 标号。第 个命题可以用两个参数 来描述，其中 ，。如果 ，那么该命题就表示第 个命题为真；如果 ，那么该命题就表示第 个命题为假。
小 发现这 个命题有一个神奇的性质，存在一种决定每个命题的真假的方式，使得这些命题在逻辑上自洽。形式化地，存在一个长度为 的 序列 ，使得对于每个 都满足 ，其中 表示异或。
然而有一天，小 B 忘记了每个 的取值。他想知道每个 在 中任意取值所得到的 种方案中，满足上述神奇性质的方案有多少种。
可怜的小 B 并不会这个问题，所以他来求助你。由于答案可能很大，他只需要你告诉他答案对 取模的结果。
。
题解
考虑一个排列 ，其逆序对数为 。
题目要求的其实是统计逆序对数 的排列个数。
设 为答案。考虑插入 的位置：若放在第 个位置，则贡献 。因此有转移： 。
这就是经典的排列逆序对计数问题的同余版本。
用 DP 或多项式生成函数均可，复杂度 。
T3-三元组（triple）
题面
给定一个长度为 的序列 ，元素从 开始标号。
定义一个由整数构成的三元组 是合法的，当且仅当它满足如下两个条件：
- ；
- 。 定义一个合法三元组 的权值为 。
次询问，第 次询问会给定一个区间 ，你需要求出满足 的三元组的最大权值是多少。
。
题解
题目要统计三元组 满足 且 。
考虑固定 ，我们要求 。
等价于在 内找到一对和为 的数。
做法：枚举 ，检查 是否出现过。用哈希/数组标记即可。
总复杂度 可以接受。若优化，可以用 或二分，做到 。
T4-秩（rank）
题面
定义一个矩阵的秩为对其高斯消元后，非全零行的个数。
定义一张无向图的秩为其邻接矩阵的秩。
给定一棵 个点的树，结点从 开始标号。你可以任意删除树上的边，请你求出这样 能够得到的 种森林的秩之和是多少。
答案对 取模。 注意，本题矩阵的所有初等行变换都是在实数意义下进行的，而非在模 意义下。
。
题解
这是一个计数问题。题目本质是：给定一棵森林，计算其秩的概率分布。
关键结论：一棵树的秩只和大小有关，设大小为 ，其秩分布可以通过递归拆分得到。
设 为大小为 的树的秩分布，则 ，其中 表示卷积。
因此整体问题转化为多项式卷积，可以用 NTT 在 时间内求出。
模拟赛题解/2025.9.26 模拟赛
· 阅读需 10 分钟
T1-留影机（camera）
题面
琴团长带可莉去湖边玩啦！
果酒湖畔的树落下了 片叶子，第 片落下的叶子的美观值为 。这 片掉落的叶子总美观值 是每片叶子美观值的积。
可莉有一个留影机和很多镜头。如果她使用第 个镜头，那么一张照片可以记录 的美观值。
由于背包容量有限，可莉只能带一个镜头，但她想要把所有的美景都记录下来，而且不想拍太多的照片。作为荣誉骑士，请帮可莉挑一个镜头 ，使得她可以用尽量少的照片使得这些照片记录的美观值之和恰好为总美观值 。
。
题解
考虑枚举 的每一个质因数的出现次数，显然 的最大值就是所有质因数出现次数的最小值。
注意到一个数 的直接出现次数为 ，所以一个数 和它的倍数的直接出现总次数就是
所以一个数的总出现次数就是
直接枚举所有质因数 并 求 ，时间复杂度为 。
T2-关禁闭（confine）
题面
这是一道交互题。
可莉又被关进禁闭室啦！
禁闭室的门上有一个密码锁，密码是一个长度为 （ 为偶数）的 串 。
可莉想要猜出密码逃出禁闭室。可莉有一个嘟嘟可，可以告诉可莉一些信息。 假设可莉猜测密码是 ，那么嘟嘟可会告诉可莉 和 的关系：
- 如果 的长度不为 或 中的字符不为 或 ，那么嘟嘟可会坏掉。
- 如果 和 对应位上相同的个数等于 ，那么嘟嘟可会返回 ，可莉可以逃出禁闭室。
- 如果 和 对应位上相同的个数等于 ，那么嘟嘟可会返回 。
- 否则嘟嘟可会返回 。
由于嘟嘟可的能量有限，可莉只能询问嘟嘟可一定的次数。 可莉不会猜密码，作为荣誉骑士，你能帮她猜到密码逃出禁闭室吗？
。
题解
考虑直接随机化，可以发现实际上 次直接随机找到符合 个位置相同的字符串的期望概率几乎是 。
考虑直接钦定一个点，对于剩余所有点，把这个点和另一个点同时反转，如果符合 不变则说明二者正确性相反。
考虑直接把相反的反转，则此时只可能是全对或者全错，两次之内一定能得出正确答案，询问次数为 次。
总询问次数刚好是 。
T3-蹦蹦炸弹（bomb）
题面
“风花节”到了！阿贝多陪可莉玩起了蹦蹦炸弹。
游戏场地是一个由 个单位方格组成的巨大草坪。每个方格用坐标 表示，表示在草坪第 行第 列位置。
可莉和阿贝多轮流操控一枚特殊的蹦蹦炸弹。每轮行动中，当前玩家可以选择将炸弹向正下方 或正右方 推动一格。
草坪上有 k 个水坑，坐标为 ，每个水坑有一条鱼，价值为 。如果炸弹被推到水坑 上，它会立即爆炸，得分为 ；
如果炸弹被推到场地外也会爆炸，但得分为 。
阿贝多先手，他希望最终得分尽可能小，可莉则希望得分尽可能大。
游戏会在炸弹 爆炸后立马结束。 对于炸弹的每个起始点 ，定义 为在双方都最优操作的前提下，最终的得分.
你只需要输出 的值。
。
题解
显然有一个 的暴力 ，设 表示到点 ，先手/后手操作的结果，那么 ，若 有水坑，。
发现状态数很多，但转移是 的，考虑优化状态数。
首先一个点由谁操作是确定的，所以状态的最后一维可以去掉。
假设当前是先手操作，转移可以转化为 ，这等价于 。发现一个水坑 只会直接影响到 ，其余的点由它右下角转移过来，那么将会被影响到的点特殊转移，剩下的点按对角线转移即可。
T4-嘟嘟可（dodoco）
题面
可莉在玩游戏！她有 个大小不同的嘟嘟可，并用阿贝多制作的小机关让它们能够自己动起来。
第 个嘟嘟可走过一单位距离需要 秒。可莉在赛道上放置了 个石碑，第 个石碑放在距离起点 的位置。
游戏规则是这样的： 一开始，所有嘟嘟可都站在第 个石碑，并且留下刻印。它们会不断往前走，直到有嘟嘟可到达了某个石碑。
这时可莉会选择到达了任意一个石碑的编号最小的嘟嘟可， 让它在石碑上留下刻印，其余未到达终点的嘟嘟可则会触发机关，被风元素气流吹回到 上一次它们留下刻印的位置（每个嘟嘟可都会触发一次机关）。
如果某个嘟嘟可在第 m 个石碑留下刻印，就算成功到达终点。剩下的嘟嘟可会从自己的刻印位置出发，直到全部到达终点。
不过，吹回嘟嘟可的机关会消耗大量风元素结晶。于是，可莉想知道：如果前 个 嘟嘟可一起玩，到最后机关总共会被触发多少次？
设 表示有 个嘟嘟可参赛时，比赛结束前机关总共触发的次数。请你帮可莉算出 的值，好让她准备好足够的风元素结晶。
。
题解
这里我们称触发机关为“传送”。
我们可以将比赛过程分为 轮，每轮有一架嘟嘟可从上一个石碑走至下一个石碑，其余的传送。
考虑每轮是哪个没有传送。发现是走向下一个石碑时间最少且编号最小的。设 表示 从 号石碑走向 号石碑所需的时间，发现实际上这个顺序是对这 个数组的归并。具体来说就是每次取这 个数组中开头最小的那一个，然后删去它，直到删空。
注意到若一个数 被删去，且存在一个 满足 ，那么 会被连续删去。证明很显然。那么可以将这些会被连续删去的合并成一个段。
容易发现每个段的段首元素单调递增，即 ，其中 为段数。
记 表示石碑 到 的距离，发现 ，而对于相同的 ， 相同，所以实际上我们在对 分段，所以可得 ，又由于 ，其中 为总距离，所以 。
考虑怎么算答案。每次一个嘟嘟可走至下一个石碑时，对答案的贡献为剩下的没到达终点的嘟嘟可个数，则答案为 ，又由于一大段会连续走过去，所以同一段中的贡献相同，只需要算每段的段首，再乘上段的长度即可。所以答案为 。 的不好算，将所有的算出来减去 的即可。
考虑优化这个计算过程。现在计算一次答案的复杂度为 ，考虑优化一个 。我们固定 ，当 有序时，发现 有单调性，那么固定 ，可以找到 的限制 ， 可以双指针求出，可以做前缀和维护 的个数。
假设我们已经算出 的答案，考虑计算 对答案的增量。分两种情况：
- 时： 增量为 ，枚举 ， 次在 的位置单点加 ， 次查询 的前缀和，可以分块根号平衡。
- 时： 增量为 ，枚举 ， 次在 的位置单点加 ， 次查询 的后缀和，也可以分块根号平衡。
模拟赛题解/2025.9.25 模拟赛
· 阅读需 10 分钟
T1-微光（glow）
题面
你设计了一种新的屏保——也是一些彩色的泡泡。为了简化模型，你决定从一维上的问题下手：你现在有一根长为 米的线段，在上面有 个泡泡，每个泡泡以 米/秒的速度，匀速沿着线段，在两个可能方向中的一个方向上移动，并以可能的 种颜色中的其中一种着色。
你设定：如果一个泡泡和另一个泡泡相碰，则该泡泡会改变方向，向着相反的方向以相同速度继续运动。此外，向左运动的颜色为 的泡泡和向右运动颜色为 的泡泡发生碰撞后，先前向左的泡泡的颜色会变成 ，而先前向右的泡泡颜色变为 。
给你所有泡泡的初始位置、颜色、运动方向，对于每种颜色，确定所有泡泡以该种颜色着色在离开线段前运动的总行程。
。
题解
改变方向太麻烦了，考虑不改变点的移动方向。
问题就转化成两个点相遇后继续向前，其中向右的点颜色不变，向左的点改为二者颜色之和。
于是向右的点的总权值是容易统计的。
向左的点可以考虑模拟这个过程，但是基于点模拟太慢了，可以基于颜色模拟，记忆每种颜色有几个点。
遇到向左的点就加入，向右的点就更改，因为 相当小所以可以暴力修改。
于是直接得到一个 的暴力做法。
T2-泪雨（namidame）
题面
给定小写英文字母和 ? 组成的字符串 。
“泪雨” 定义为这样的串：这是一个回文串，并且 ? 的个数大于等于小写英文字符的个数。
请对于是 “泪雨” 的 的所有子串，求出它们问号位置的和之和。（位置下标从 开始）
形式化题意：定义：
请你求 ，其中 。
。
题解
先找出回文串然后考虑如何算贡献。
对于一个符合泪雨性质的子串，我们注意到因为它是一个回文串，所以其问号的位置之和即为问号数量乘以其中心位置。
而 维护的就是对于一个点，以其为中心的最大回文串长度。
所以可以考虑在 过程中维护以该点为中心的所有“泪雨”串的问号数量之和。
对于一个点，我们可以跟 一样从其对称点进行转移。
考虑到可能出现超出当前右边界的情况，我们注意到可以直接向内减小字符串，于是暴力收缩。
这样的复杂度其实是正确的。记回文半径为 ，从 处转移，我们考虑当前最右的区间 ，我们在 时就更新回文区间和对应中心。当 时发生收缩，总的收缩长度：
如果发生了收缩， 就会变成 ，所以 ，复杂度是对的。
复杂度均摊 。
T3-深海（sort）
题面
小葱很好奇一个序列冒泡排序 轮之后的样子，具体地说，对于一个长度为 的排列 ，她有两种询问：
1 给定 ，求将 的区间 冒泡排序 轮之后， 这个数在数组中的下标。 2 给定 ，求将 的区间 冒泡排序 轮之后， 的值。
定义对 的区间 进行一轮冒泡排序为：依次对 操作，若 则交换 。
注意询问中的排序操作并不实际在 上生效，也就是说询问之间互相独立。小葱不会为难你，所以对于单个测试点，所有询问都是同一种。
。
题解
O=2
研究排序问题时（尤其是排列），可以先进行值域压缩：通常我们会把序列变成 - 序列，比较特殊的时候还会有压缩成 或其它更大一点值域的需求，在此不展开。
我们二分值域，随后把序列变成 ，接下来只需要判定询问的位置是 还是 。
考虑刻画一下冒泡排序的操作。对于下标从 到 的序列：
现在 之间没有区别，我们完全可以让最左边的那个 不断交换到最后，也相当于把最左边的 之后的下标减 再把它的下标设成 。注意一些边界，那么判定就是很简单的：
- 如果 序列中 的个数，那么显然序列已经排序完了。（不用特别划这个）
- 如果 ，那就说明出时它在长度为 的后缀上，只需要判断 的数量是否足够。
- 其余情况，我们只用数一下 前面有多少个 ，若只有 ，则答案显然就是 ；否则，答案就是绕过了长轮子移后到达 位置：。
对于区间询问，进行主席树上二分即可做到 。
O=1
由于涉及了具体的位置，我们不妨把值域压缩成 再观察（其实可以脱离值域压缩观察，因为只涉及和 比大小）。我们考虑 的动作。
首先，当前面有1时，和 一样，它的行为和 一致，每次会向前移动一步；当前面没有1的时候，它向后冒泡，直到遇见一个1，之后这个1就会向后冒泡。
同样地，考虑形式化这个东西：
- 如果 序列中 的个数，那么显然序列已经排序完了。
- 先统计现在 的位置前有多少个1，记为 的情况是平凡的，现在还要向后移动 次，代表我们要找到从左到右数的第 个1的位置，计算答案直接做。
- 否则较复杂，换句话考虑，考虑后面有多少个1会移到它前面，就是要知道的是从 的位置到 ，这样就做完了。
这一部分可以离线后扫扫描线，主席树即可。
时间复杂度 。
T4-虚无（nihility）
题面
你正在玩一种智力游戏，你需要让在迷宫起点处的棋子到达终点。
坐拥上帝视角的你已经知道了迷宫的全貌，这是一个 个点 条边的有向图，每条边有一个颜色 ，一个点连出的边颜色都不相同，且图中所有边的颜色只有 种。为了方便，我们把起点标号为 ，而终点为 。
这个游戏的流程是这样的：你有一个牌堆，在游戏最开始的时候，你可以向牌堆里加入任意多的牌，每张牌有颜色，颜色由你决定（在 中）。随后游戏开始：
假设当前棋子处在点 ，当前牌堆顶的牌颜色为 ：
1 如果 向某个点 连了一条颜色为 的边，就把棋子向点 移动，并丢弃牌堆顶的这张牌。 2 否则，若牌堆为空或者不存在一条出边颜色为 ，你可以把棋子沿着该点任意一条出边移动。如果选择了一条颜色为 的边，则会在牌堆顶加入一张颜色为 的卡牌。
为了让游戏有挑战性，你想要让初始牌堆的牌数目尽可能少。你只需要求出这个最少的数目。
，对于输入的每条边 ，保证 。
题解
如果可达，那么答案必然 ，考虑在起点前加一些“没有限制”的虚点，以此使得可以在起点 获得所有可能方案，我们这样连边：
- 对于 号点，向 连所有颜色的边。
- 对于 向 连所有颜色的边。
没有限制的意思就是说：这些边只负责加牌，而不执行操作 。
这样如果我们能够从虚点 以空栈状态到达 ，答案就是 （若从 能到答案就是 ）。
现在问题转化成了一个可达性问题，我们只需要判定是否空栈地从起点，以空栈的状态到达终点。
注意空栈任选走边加牌到非空栈时强制走边这个过程比较特殊，我们需要在状态里加入这个信息。
记 表示，存在一条路径使得空栈状态的 可以到达空栈状态 ，且，路径中不存在在一个空栈的时候有颜色为 的出边。转移考虑类似括号序列生成的转移。
第一种转移形似传递闭包，也可看作把两个括号序列拼在一起：
第二种转移仅在括号序列两侧加一对括号：如果 有一条颜色为 的入边 ， 有一条颜色为 的出边 ，且 不存在一条颜色为 的出边， 。
注意此类转移对我们建的虚点也生效，因为它们没有要强制定之类的限制，也就是 时也执行转移。
注意一种情况：当前可能用满所有颜色边的时候（其实就是 连出了所有颜色的边的时候），我们新建一个颜色 ，即用解作这种情况。
转移顺序比较复杂，使用记忆化搜索即可。时间复杂度 。
题解：P14059 【MX-X21-T4】[IAMOI R5] 使一颗心免于哀伤
· 阅读需 2 分钟
题目链接
题意简述
有一个由 组成的环，每次知更鸟可以删除一个由 组成的连续段，星期日可以删除一个由 组成的连续段。
最后唯一剩下的颜色对应的一方落败，求双方都选择最优策略的情况下最终哪一方获胜。
解题思路
官 sol 已经给出了结论做法，在此处考虑模拟博弈过程。
发现可以把连续段缩成一个同色点，因为给出的是一个环，所以最终得到的环一定是形如 的。
每一次操作，如果使一个连续段消失了，就会删除一个 段，此处显然两人都想要使 段数量保持在偶数。
我们发现，如果想要不使一个连续段消失，只选一个点一定最优，因此我们可以记录可使所有连续段都不消失的最大可删点数，即 （其中 是连续段个数， 是第 个连续段的长度）。
同时，每次删除连续段的操作都会使对手的可删点数 ，于是我们模拟这个博弈过程，进行决策即可。
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 100005;
int T , n;
char s[N];
signed main()
{
cin >> T;
while(T--)
{
cin >> n >> s + 1; int cnt = 0 , R = 0 , S = 0;
for(int i = 1 ; i <= n ; i++)
{
if(s[i] != s[i - 1] || i == 1) cnt++;
else (s[i] == '1' ? R++ : S++);
}
if(s[n] == s[1]) (s[1] == '1' ? R++ : S++);
int now = cnt >> 1;
if(cnt == 1) {cout << (s[1] == '1' ? "Sunday" : "Robin") << '\n'; continue;}
while(now)
{
if(now == 1) {cout << "Robin" << '\n'; break;}
if(now & 1) now-- , S++;
else if(R) R--;
else now-- , S++;
if(now == 1) {cout << "Sunday" << '\n'; break;}
if(now & 1) now-- , R++;
else if(S) S--;
else now-- , R++;
}
}
return 0;
}
模拟赛题解/2025.9.23 模拟赛
· 阅读需 10 分钟
T1-小 X 与宝藏（treasure）
题面
小 游山涉水，想要找到埋藏在深林中的宝藏。
他偶然得到了这个深林的藏宝图，深林可以被看作一个 的矩阵。宝藏在地图中以 “” 被标记出来，与此同时其他地方都是 “”，同时宝藏的个数为 ，奇怪的是地图上并没有标明它描述区域的具体方位。
深林中有两条大河，一条是纵向的，一条是横向的。由于陆上的宝藏都已经被人他们开采完了，小 只好转而寻求埋藏在两条大河深处的宝藏。可他并不知道大河具体在哪，也不知道大河的宽度有多少，地图上也没有标明。他唯一确定的，是两条大河横跨整个深林。
他通过小道消息得出两条大河中的宝藏的个数之和为 。他想动用大批人马，对所有符合条件的地下进行搜寻。请你帮小 统计大河位置情况的方案数。
如即是两条大河的合法位置，注意大河方向一个为横，一个为纵，且长度都是无穷大的，宽度至少为 。蓝色和黄色分别表示了两条大河，注意它们相交的绿色区域被计算了两次贡献。
。
题解
法一
发现两条河的宝藏数是可以分开计算的，于是对于原矩阵维护一个二维前缀和和后缀和，这样宝藏的数目就可以在两个点对上统计贡献，枚举其中一个点对，用数据结构寻找另一个点即可。
复杂度 。
法二
容易发现可以 枚举其中一条大河的宝藏数量。
直接 NTT 求对于不同行，某个宝藏数量的方案数，。
因此时间复杂度为 。
T2-小 X 与数字（number）
题面
小 有 个非负整数 ，其中 。 小 很喜欢不一样的数字，但是不喜欢很大的数字，所以他希望 的值两两不同，他认为满足这个限制的数列 是好的。 给定 , 和 , 你能帮他求出好的数列的个数 的结果吗？
。
题解
考虑 取到 的方案数，不难发现为 。先考虑 ，则此时任意一个排列的方案数都是 。
设 。考虑拆贡献，用乘法分配律展开，钦定 选择了 ，那么为它们分配 的方案数是 ，其中 $$ 是把所有 从小到大排序的第 个，而剩下的位置的方案数为 ，直接乘起来就是这种钦定的总方案数。
设 是按 的顺序排好的， 为考虑完前 个 ，钦定了 个的答案之和，这里的答案不算 的部分。那么 的转移为 。
最后答案为 。
即可。
T3-小 X 与序列（seq）
题面
给定一个 个点的无根树，每个点有一个标号 。
定义一条链 的权值为按照从 到 的顺序把这条链的标号写下来之后，得到的序列的最长上升子序列长度。
你需要删掉一个点，使得剩下的链的权值的最大值最小。
。
题解
先考虑怎么算出整棵树的 。
求 一般是用一个栈来维护每种长度的结尾最小最大是多少，在树上也同样可以这么做。并且栈的长度不超过深度，所以显然可以长链剖分优化。
然后注意到删点必然是删当前最长的一条链上的点，否则没有效果。
从链的两个端点分别跑一遍长剖，就可以算出删每个点的答案了。
T4-小 X 与停车（parking）
题面
小 在一家饭店的停车场工作，她负责礼貌地接待重要的客人，保管他们的车钥匙并帮助他们停车。
一个晚上，她发现她管理的停车场中恰好有 辆车，它们共有 种不同的颜色，每种颜色恰有两辆车。我们将颜色按 到 编号。
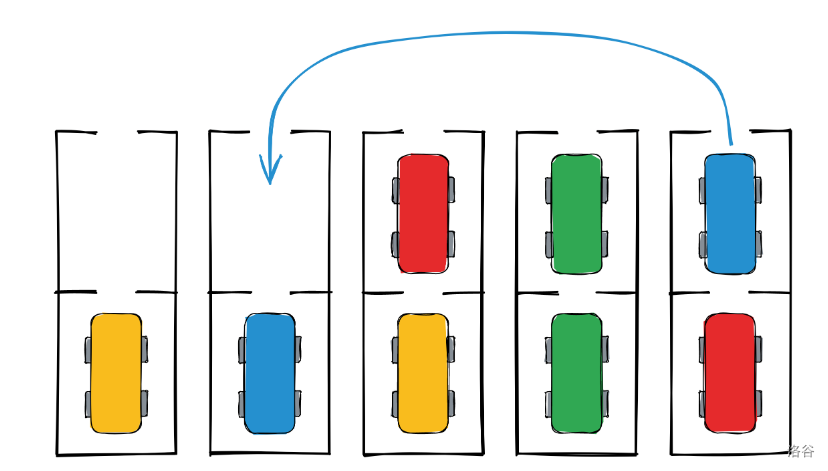
这张图描述的是一个样例，同时呈现了唯一的第一次驾驶。
停车场共有 个车位，按 到 编号。每一个车位可以停下两辆车，一个车位只有一个入口，我们称靠近入口的为「顶上的车」，远离入口的为「底下的车」。一辆车可以从入口开出当且仅没有车挡着它。小 在停车的时候，保证每个车位要么空，要么停满两辆。要么只有一辆底下的车。
小 想要重新停放车使得每一对相同颜色的车都在一个车位里。我们并不关心车位对应什么颜色以及哪辆车在顶上哪辆车在底下。小 将执行如下操作：
- 驾驶一辆可以驶出车位的车，将车开到另一个车位，满足：
- 这个车位是空的，并把车停在底下的车位，或者，
- 这个车位有且只有一辆与当前驾驶的车颜色相同的车。 小 想知道最少的操作次数与操作方案，请你解决这个问题。
如果操作次数正确，但方案构造错误，将得到 的分数。
。
题解
若一个栈的栈底为 ，栈顶为 ，则称其为 。
首先如果栈的两个颜色相同，则不会管它们了，不可能会把其中一个挪到一个空栈。每操作一次也最多匹配一个颜色。
假如其中一个栈 满了，设其为 ，则 要动的前提是把 挪走了。我们用一个有向图刻画，对于这种情况我们连边 ，这样每个点的出度和入度之和每时每刻都 ，这使得该图的形态很单一，可以尝试对每种形态逐一攻破。
在分析之前，我们要找出了一个颜色 和其它颜色 有连边说明有一对 在同一个栈中。如果 的两个度数不全说明有一个独占一个栈，即 。
- 孤立点 （度数为 ）
设其为 ，则可以将 操作一次变为 。这样只用一步，不仅匹配了 ，还多了一个空栈。绝对是不亏的。
- 一条局部链（链上的点恰恰的点没有连边）
设其为 。
首先我们无法到孤立点x的贡献：只用一步，匹配一种颜色的同时，多出一个空栈。
我们发现 的分布是 和 ，则我们可以变成 和 ，在匹配 的同时去掉了 这条边。我们可以一直这样做直到变成孤立点，这样在不借助其它栈的同时用 步将栈删完，还多出一个空栈。
类似的，只要存在入度为 ，出度为 的点，都可以通过这种方法一步一步匹配。我们可以用类似拓扑排序的方法将位于链上的点消除。
剩下入度为 的点出度均为 ，所以我们有以下情况：
-
个点 条边的环（即连通块中出度和入度均为1）。
-
一条非同向链，形如 ，可以视为若干条有向链的两端点拼接得到，尾两端点均为链尾。
-
非同向链的两端点合并。
此时不同点都无法直接用一步匹配，只能在环或者非同向链上消除。移动的限制也说明了不能在两两端点之间消除，所以我们必须要先找到一连通块消耗掉的步数和额外的空栈，操作的实质已经不离散于之前的操作。此时我们必须要有至少一个空栈，否则没有合法方案。
- 个点 条边的环
考虑合成，将环拆成两个栈为 ，此时我们必须找到一个空栈 ，将这两个栈变为 。这样我们将环花一步操作拆开，并多了一个空栈。我们接着把 这条边，设为 ，拆掉一个环，剩下的部分还是环。我们可以再这样继续拆，直至最后只剩一个栈，没法继续操作，已经是当前最优的方案，所以只要能优先清去，不会对其贡献的分产生影响。
- 一条非同向链}
此时我们要考虑从出度为2的点处断开，设其为 ，则形如 ， 和 连出了两条链，此时 所在栈为 ，存在一个空栈 。
此时，如果两端的链中有一条是有向链（这种链一定存在，就是最靠近链尾的两端的出度为2的点），设这时 所在的链是向链。则可以用1步将 变为 ，消除 的边。剩下的按照前述方法又会还原一个空栈，并且相同的时候链长度减小，效果和环不一样，甚至还在最后增加一个空栈。优先进行这种操作肯定不亏。
- 非同向链两端点合并
此时我们不妨不将两个出度为2的点 ，其为 ，通过 变为 ，这里要留1步才行，消去一个空栈，将剩下的安排为向同向链。这额外的1步和一个空栈不得不使用，但后续的清除时，所以它应放到最后处理。
只要模拟这样的过程即可，复杂度 。
模拟赛题解/2025.9.22 模拟赛
· 阅读需 10 分钟
T1-题意（orchestra）
题面
给定一串长度为 的数对序列 ，其中 都是整数。
有 次询问，每次给定两个整数 ，你需要先选定一个整数 （注意 可以为 ），然后再选定一个正整数序列 （若 则该序列为空），使得
最大，输出这个最大值。
。
题解
首先把 提出来，发现此时 部分固定了。
并且 的值域只有区区 ，于是我们考虑用类似于背包的方式，用 表示 的时候 的最大取值。
最小值最大容易想到二分答案，于是二分判定是否可行。
复杂度 。
T2-戏已完结（plaudite）
题面
给定两个正整数 ，其中 。
我们称长度为 的非负整数序列 满足以下条件是良好序列：
- 。
对于一个良好序列 ，定义函数 ，其生成的序列如下：
即将序列 进行升序排序后得到 。
接下来有 个询问，每个询问给定 ，求：
- 计算所有可能的良好序列 对应的 中第 个元素的总和，并输出该值对 取模后的结果。
tips：可能对解题有用的定理
在一个 的网格中，我们称 这一步为一个横线，所有 （只能向上或者向右走）的路径中，设恰好有 条横线在 直线上方（即横线两端点均在直线上或上方）的路径有 个，那么所有 相等。
。
题解
考虑转化成一个格路计数问题：
- 有一个 的网格，每次可以往上或往右走，要从 走到 。
- 每次从 就确定了 ，称 为斜线。
- 对于某个 ，可以转化到斜线：画出 的所有斜线，对于每条斜线，若有一个横线在它的上方经过，则将 加上 1。
考虑对于每条斜线贡献时，我们想要求对于每个 计算，有多少个方案恰好有 个横线在它的上方经过。
先将对路径斜线转化为路径斜线的情形，这部分贡献可以 算出。
枚举某条斜线上的前两个位置，设这这是路径的第 次、最后一次触碰斜线的位置。
我们有结论：
- 在一个 的网格从 走到 ，设所有 在对角线上方经过的次数为 的方案数是 ，则所有 相等，均为 。
于是设定第一次、最后一次触碰斜线位置后，可贡献的 是一个区间，因为区间中的每个 贡献相等。
直接枚举答案复杂度是 ，考虑如何优化。
把 的直线分成 和 两部分。 和 是对称的。
考虑 的部分。
假设我们枚举了触碰起始点之间的长度 ，则任意分数组上的修改位置是确定的。
枚举 ，那么段触碰起始点之间的方案是固定的，前后两段的形式都是 且不触碰 的折线计数（假设把后一段对称一下）。
把这两段拆开挂起来，就变成了一段折线，形式也是 且不触碰 ，且 是很左很左的点。这部分的方案数就变成了两个组合数根据 的形式。
再枚举所有的 加起来，发现加和的式子能拆掉，可以 计算同一个 的方案数。于是这部分能做到 。
考虑 的部分。
由于我们只需考虑分数组上修改权，所以可以只关心：对于所有触碰起点 点，其方案数之和，起点和终点由 决定，不再考虑起点。
由于起终点之间的方案数就是 的形式，我们代入这些部分全部在斜线上面走。那折线就变成了从 到起点是走最短路径，走上去到 并且不穿过斜线。
这样也是两段 不触碰 的形式，可以把两段折线拼起来，贡献就是两个组合数相乘。
枚举所有的 加起来，发现要求若干个如下的形式：
观察一下，发现上面加起来是常数，下面加起来也是常数。把这个看作要求
先考虑 。若考虑 ，则 不会修改， 有 的变化，于是式子可以 维护。
增大了，显然只需要加上一项。
- 增大 的话，考虑这个式子的组合含义是在 个白球中染黑 个，且第 个黑球的位置 。 若 ，限制变成第 个黑球的位置 ，需要减少第 个黑球位置 的情况。
于是这部分也能做到 。
T3-运输规划（xor）
题面
在数轴上依次排列着 个工厂，从左到右第 个工厂有 单位货物。
商人蛋蛋拥有 种货车，编号为 。若使用编号为 的货车运输 单位货物，则能获得的收益为：。
其中 表示按位异或， 为给定常数。
现在有 次独立的运输计划，对于第 次计划，蛋蛋只知道货车会前往某个工厂，工厂编号在区间 之间（包含两端）。在计划开始前，蛋蛋可以从所有货车中任选一种。
蛋蛋想知道：在最优选择下，每次运输在最坏情况下会获得多少收益。
。
题解
肯定不能枚举端点。考虑在 trie 树上干点什么东西。令 为 trie 树上节点 的答案， 为其深度，则：
f_p = \begin{cases} \max(f_{ls}, f_{rs}) & (ls \wedge rs) \$$6pt] f_{son} + 2^{m-dep_p} & \text{otherwise} \end{cases}答案就是根节点的 dp 值。
枚举左端点，移动右端点，加入一个点只会修改 个位置的 dp 值，。
再进一步，直接莫队，。
相比 很小，考虑从 下功夫，即每个位置对答案的贡献。
换一种方法描述上面的 dp：选择一个值，从 trie 树上代表这个值的节点一直往上跳，没有兄弟就把和加上 ，求最⼤邻和。
显然这个值只会存在于区间内，因为空节点的 dp 值一定为 。
对于 的深度为 的祖先的兄弟，设这个兄弟子树内点的集合为 ，则区间需要包含 而不包含 内任意的数， 对这个区间的贡献的第一个 位才是 1。显然我们只需要知道 里的前驱与后继 ，区间的范围为 。
因为只有两个祖先，所以只有两个对 ，所以对于一个 ，把所有区间分成了 种不同的贡献（左边 种，右边 种）。一个相同形式区间记作 。这个限制并不好做，因为涉及到 。但是不难证明直接按 做是对的。因为缩小区间会使实际答案变⼩，而不会变⼤，一定不优。
于是直接扫描线，。
最后考虑用分块平衡，做到 。搞笨的，直接树状数组差不多能直接过（官方数据并没有卡，感觉也难卡，所以干脆放了）。
其实要慢代码慢的地方是 的双 vector 遍历。
T4-不吼不叫（string）
题面
小 A 有一个初始字符串 。他希望通过一系列操作将 转换为目标字符串 。每次操作，他可以选择切掉 的一个前缀或一个后缀，但必须满足以下条件：切掉的前缀或后缀必须是操作后剩余字符串的子串。也就是说，如果切掉前缀 后剩余字符串为 ，那么 必须是 的一个连续子串；同样，如果切掉后缀 后剩余字符串为 ，那么 必须是 的一个连续子串。
小 A 想知道最少需要多少次操作才能从 得到 。如果无法通过任何操作序列得到 ，则输出 。
，字符集 。
题解
正难则反，将切除操作改为添加，很显然尽可能大地添加字符段最优。
所以维护 表示以 为右端点的最长公共后缀，同理维护 表示以 为左端点的最长公共前缀。
同时，维护 表示区间 能向左/向右添加的最长段落长度。
从 在 中的子串位置开始，做一个类似多元最短路的操作即可。
复杂度 。
模拟赛题解/2025.9.19 模拟赛
· 阅读需 7 分钟
T1-逆序对（inv）
题面
给定长度为 的正整数序列 。
次询问，每次给出 ，求 ，满足 ，，若不存在满足条件的 则答案为 。
为了减少输出量，你只需要输出 次询问的答案的异或和。
。
题解
不难发现只需关注每个 与其前驱（最大的 满足 ）。
证明：考虑按顺序的三个元素 ，其中 ，则 不可能成为答案：
若 ，则前驱是 ；否则是 。
记 的前驱为 ，扫描 从左到右，时刻维护每个 的答案。只需要在 移动的时候令对应位置取 即可。
容易使用树状数组等数据结构维护。
复杂度 。
T2-一二三（yes）
题面
给你 个数 ，其中 ，每个数还有一个权值 。
你可以进行如下操作若干次：
- 选择一段区间，满足这段区间的 之和为 或 ，将这段区间删除，并合并剩下的序列。
你希望剩下的数字的 之和尽量小，如果有多种不同的方案，求出 之和最小的条件下， 的最大可能和。
你需要输出对应的 之和与 之和。在有些子任务中，你要给出方案。
。
题解
考虑怎么判定是否能完全删除某个序列。
不妨先找出一些必要条件，显然 。在满足这个条件的基础下，不难发现如果 ，则一定能完全删除，因此关键在于如何删除 。
删除 的方法只有 3+1，3+3+2，3+5 三种，不难发现其中 的部分的和大于等于 的个数。因此另外一个必要条件是 。可以构造性证明满足这两个必要条件就是充分的。
先考虑如何计算答案。记 表示对于序列 ，如果最后留下了 ，那么最小的 之和是多少。转移枚举 满足区间 可以被完全删除，求最小的 。容易使用树状数组等数据结构加速。复杂度 。
构造考虑先尽量删除所有 3+1 和 3+3+2，此时序列一定形如 ，任意删除一段能删除的即可。
可以用一个栈维护现在的序列，如果栈顶的一段元素和为 或 ，并且删掉这一段之后仍满足必要条件，就可以直接删掉。构造时间复杂度是 的。
T3-黑白树（tree）
题面
给你一棵 个点的树，你要把每个节点黑白染色，定义它的丑陋程度为：
- 所有的连通块中，黑点和白点个数差的绝对值的最大值。
你希望它的丑陋程度尽量小。在这个问题中，你要解决三类问题：
- 求出最小的丑陋程度。
- 求出最小的丑陋程度，并且构造方案。
- 你需要额外保证黑点和白点的个数之差不超过 。求出满足这个要求的最小丑陋程度，并且构造方案。
。
题解
先找出答案的下界。
记叶子个数为 ，考虑所有非叶子与黑叶子构成的连通块，先删除所有黑叶子，再加入所有白叶子，值域变化为 ，因此答案至少是 。
有经典结论是可以使用 条可以相交的路径覆盖所有点，构造直接将叶子按 dfs 序编号，前一半和后一半按顺序匹配即可。那么可以将原树划分为 个集合，每个集合是某条路径的子集。
把每个集合按照路径顺序黑白染色即可。一个连通块与一个集合的交集一定是连续的一段，因此黑白点个数之差不超过 ，总共 个集合，因此最大黑白点数差不超过 。
可以根据当前黑白点个数决定下一个集合是先染黑色还是先染白色，保证整体黑白点数差不超过 。 集合划分时，不妨依次考虑 条路径，将路径上未划分的点都划分进当前集合。容易使用并查集维护，或者找到所有叶子的重心后 dfs 维护。
复杂度 。
T4-抽卡牌（card）
题面
有 种不同的卡牌，第 种卡牌共有 张，你希望获得 张这种类型的卡牌。
初始所有卡牌都在卡池中，每一轮你会从卡池中的所有卡牌中随机抽取一张。设抽中的卡牌类型为 ，如果你已经有 张该类型的卡牌，则你会将这张卡牌重新加入卡池，否则你会拿走这张牌，这张牌之后不会再进入卡池。
如果你手上每种卡牌的数量都达到了 个的限制，游戏会立刻结束。求出游戏的期望轮数，对 取模。
。
题解
考虑将这个无限过程改为有限的。若你抽出了一张牌 时，已经有了 张同类型牌，则视为将这张牌加入弃牌堆。若你手中已有 张牌，弃牌堆中有 张牌，则再抽出一张牌的期望时间为 。
此时整个随机过程就可以被视为一个由 生成的多重集排列， 种排列都是等概率出现的。考虑计算 表示 这个状态在所有排列中出现的次数。
不妨枚举 表示第 种卡牌已经抽出了多少张，则根据多重集排列，方案数是：
其中 ，因此考虑在 dp 过程中计算上式分母乘积。
记 表示前 种卡牌中，此时手里有 张，弃牌堆里有 张。转移枚举 ， 加上 ， 加上 。注意要扣掉满足所有 的方案。复杂度 。
优化考虑 中分母只与 有关，在 dp 时可以直接记录 ，对分子的两项分别考虑。 这一项是简单的，最后乘 即可， 这一项相当于在所有 中选择了一个乘上去，dp 时多记录一维 01 即可。
复杂度 。
模拟赛题解/2025.9.18 模拟赛
· 阅读需 8 分钟
T1-长城（test）
题面
一个长为 的序列 被称为墙壁序列当且仅当满足下列条件：
- 对 ，有 。
- 中所有数的异或和为 。
给出 和 ，求出有多少个长为 的墙壁序列 满足 。答案对 取模。
。
题解
注意到一个朴素的思路是第一个数任意选，之后每个数和前一个不同，最后一个固定。
显然会多算最后一位和倒数第二位相同的情况，但此时前 位 和为 。
于是我们设 固定时，前 位和为 的情况数为 ，得到递推式：
此时有两种做法：
- 矩阵乘法维护 和 进行转移，矩阵快速幂 。
- 考虑打表，发现一个神奇性质：若设
复杂度同样是 。
T2-网线（wire）
题面
给定一个字符串 ，设其长度为 ，每个字符要么是 要么是 。
定义一个片段为 的一个子串 满足下面三个条件：
- 或者 ；
- 或者 ；
- 。
定义一次变换为：选择 的两个相邻且长度不同的片段，改变长度较小的那个片段的所有字符为其相反字符。（ 变为 ， 变为 ）
现在有 次询问，每次询问会给出只包含 和 并且长度相同的字符串 ，请你判断 是否能够通过若干次变换得到 。
。
题解
注意到每次操作就是把较短的连续段合并进较长的连续段中，所以我们用链表维护连续段。
如果对于 中某一位 ，，除非 且 ，否则一定不可能到达。
除此之外，对于某个 和 相同的连续段，尽量向两边合并显然不劣，因此我们从左向右扫，直接尽量合并。
注意到连续段个数不超过 ，并且每次合并减少一个，因此复杂度为 。
T3-里斯（lis）
题面
多组询问，每组给定三个整数 、 和 。
设 是 的一个排列。若 满足以下所有条件， 则称其为墙壁排列：
- 的最长上升子序列的长度不超过 。
- 。
请计算墙壁排列的个数，答案对 取模。
。
题解
考虑 Dilworth 定理，先把题目改成：要求排列 的最小上升子序列剖分 ，并且 的方案数。
对于上升子序列剖分有一个经典算法：每次选择末尾最大的一个可以接下一个元素的子序列接下一个，如果没有就新建一个。 如果按这个流程，则每次都会有一个子序列的末尾为前缀最大值，每个元素比其大才会放进对应的子序列。
所以就把前缀最大值放进一个子序列，别的放进另一个。接下来还需要分析性质： 选定前缀最大值为 后，至多对应一个合法排列。
存在的条件是：对于所有 有 。额外性质：所有前缀最大值 必然有 ，其余位置有 。
比较难的一步转化：把前缀最大值的直方图画出来，条件等价于直方图的轮廓线一直在 上方。
若有 ，则 为一个前缀最大值，可以两边做反射容斥；否则考虑逆排列 ，求满足 长度 且 的 ，就化归了。
最终复杂度 。
T4-上课（lesson）
题面
小墙壁在大学里报了两门课，分别在两个不同的教室上课。第 门课有 节，第 节的上课时间是 到 （不含两端）。保证同一门课的上课时间互不重叠，但是两门课之间的上课时间可能重叠。
小墙壁非常强，只要某节课中的任意短的一段时间范围中（不能为一个时间点），他在上这节课的教室内，他就必定能听懂这节课的内容。然而，他需要 的时间从一个教室走到另一个教室。时刻 时，他在第一门课的上课教室。小墙壁想问你，通过合理地在两个教室间往返，他最多能够听懂几节课？
。
题解
将每个 增加 ，这样只需要在整数 的时刻转场即可，可以钦定转场时间为整数。
首先考虑高复杂度 dp。设 为 时刻在 号教室，之前最多上几节课。 如果上个时刻还在该教室，可以直接转移。但如果刚刚经历转场，直接用 转移可能是错的，因为可能把现在正在上的课算了两遍。
可以用贪心解决：如果之前在教室 的最后时刻，现在在上的课已经开始，那不如提早前往教室 的时间，因为待在教室 不能获得更多收益。 所以可以钦定不会在教室 上两次同样的课。
如果现在正在上的课开始时间是 ，就用 来转移，其中 是在教室 新听的课数， 表示教室 是否在上课（如果不在上课，就无此限制）。
显然 随 不减且最多为 ，且只有 的位置是有用的。
考虑从时间维上扫描线，动态维护目前 的大小及之前的信息。
第二类转移的限制可改为：对于某个 ，如果教室 在 时刻在上课，并且这节课在 时刻下课，那么 只能在 时刻开始才能贡献到其他状态，否则只要 时刻就可以。
对于转移中的 ，可以拆成目标时刻 前已上课数减去时刻 前已上课数，所以只需要记录最大的 减去时刻 前课数。
转移方程发生变化只会是以下几种情况之一：
- 一节课开始；
- 一节课结束；
- 一个新的第二类转移被允许；
- 时刻前一节课开始（因为第二类转移中的 会增加一）。
总量是 的。用 按时间顺序更新转移即可。
另一种做法是尝试从小到大依次二分出 的位置，或者直接设 表示在教室 ，时刻 ，对面正在上的课是否上过，这些做法也都是可行的。
模拟赛题解/2025.9.16 模拟赛
· 阅读需 10 分钟
T1-王哥与荷塘（fish）
题面
荷塘是一个平面直角坐标系，其中有 条鱼，编号为 ，位置用一个点 表示（可以重复）。它们听路过的王哥提到 “平面最远点对”，于是想亲身实践一下——进行 次操作，每次为以下两种之一：
- 充分发扬鱼类智慧，将编号在 中的鱼的位置绕原点逆时针旋转 。
- 询问编号在 中的鱼两两之间（包括自己和自己）的最大曼哈顿距离，即：
由于鱼的记忆只有七秒，难以进行大量的运算，所以它们想请你帮忙给出答案。
。
题解
首先考虑将曼哈顿距离转化为切比雪夫距离，此时只需要维护 分别的 。
注意到每次操作实质上是使 。
因此只需要用线段树维护 ，表示旋转次数，维护区间最大/最小 。
T2-王哥与演出（oblivious）
题面
王哥将要带领乐队成员在一个 行 列的舞台上演出。为了增加节目效果，她决定在 个装饰品中选择一些来装饰舞台。根据讨论，她们确定了每个装饰品在舞台上的预设位置 和记忆值 。她将通过两轮选择来确定这次演出最终的装饰品：
- 第一轮，在每一行中至多选择一个装饰品。
- 第二轮，在每一列中至多选择一个装饰品。
注意，两轮有先后顺序，并且要求第一轮选择的物品在第二轮中不能再被选择。
定义一场演出的记忆值为选择的所有装饰品记忆值之和。王哥希望乐队成员和观众都能记住这场演出，于是请你帮助她最大化这场演出的记忆值。
。
题解
考虑图论建模。把每一行、每一列都视作一个点，把饰品视为边，我们会得到一个 个点， 条边的图。若有一张第 行第 列的饰品 ，那么就视作一条连接 和 ，边权为 的边。
用选择饰品的的过程将边定向。在第一轮中，在第 行取走第 列的饰品，就将边定向为 ；在第二轮中，在第 列取走第 行的饰品，就将边定向为 。
对于一种合法的选择方式，考察定向后的建出的新图的性质。容易发现一个结点的出度不超过 ，那么整个新图就是若干棵树与内向基环树的组合。最后将边转为无向。
要求权值最大化，就是对每个连通块求出最大生成树，或者最大生成基环树。可以仿照 Kruskal 算法贪心地取边，与一般的 MST 相比只需要额外判环。
时间复杂度 。
T3-王哥与序列（array）
题面
有一个长为 的序列 ，王哥认为一个序列是优美的，当且仅当序列中所有数都相同。但是序列 初始时很有可能不是优美的，所以王哥想让其变得优美。
定义一次操作为：选择三个整数 满足 ，将区间 内的所有 都加上 （ 可以为负数）。
王哥想问你，最少用多少次操作，可以使序列变得优美。然而王哥认为这太简单了，所以他还想知道，在最小化操作次数的前提下，有多少种不同的操作方案能使得序列变得优美。
两种方案不同，当且仅当存在一个 使得两种方案第 次操作的三元组 不同。特别地，不进行操作也可以算一种方案。答案对 取模。
当然，如果你只知道第一问的答案，王哥也会给你一部分分数。
。
题解
设差分数组 ，转化为在 上考虑。每次可以选择 让 加上 ，或者选择 让 加上 ， 减去 。
考虑图论建模，如果一次操作选择了 ，就是连 的自环，如果是 ，就是 的无向边。可以发现，在最优策略下，对于一个大小为 的连通块：
-
如果这个连通块中的 都为 ，那么一定会连 条边，即形成一棵树；
-
否则一定会连 条边，即一棵树加上一个自环，相当于先操作一个数让连通块的和为 ，然后变成上面的情况。
那么求最小的操作次数，相当于将 划分为几个不交的集合，最大化集合内元素和为 的集合数量 ，答案就是 。于是可以子集 ，设 表示集合 最多划分为多少个元素和为 的集合，复杂度为 。
接下来考虑如何求方案数，设第一问答案为 ，我们求出不同的操作集合有多少种可能，最后乘上 。对于一种最小操作次数的集合划分方案，考虑每个集合 ，如果 ，那么可以发现每一棵树树对应了一种方案。具体地，对于一棵树，我们可以任选定根一个根，然后对于所有连接叶子节点的边动过几次确定操作的权值是什么，进而可以依次往上确定每个操作的权值是什么。所以方案数为 。
对于 的集合，我们将这些集合一起考虑。而对于一个自环，可以看作是和 之间连边。于是我们可以把 这两个点当成一个连通块，那么一个方案可以看作是集合 和 连通块的成的一棵树，根据 prufer 序列，方案数为 。设 表示在最大化元素和为 的集合数时，有多少种划分方案。于是第二问也可以 回答。
接下来考虑第三问，对于第一问，事实上我们不用枚举子集，只需要转移 即可。但如果这样转移会有一个空集重置，于是我们记录一个 表示集合 ，和不为 的集合大小为 ，元素和不为 的子树经过的。当 元素和为 时，我们只用 去掉集合中最小元素标号的集合来更新；然后对于所有 ，会被算重 次，所以要 。
时间复杂度为 。
T4-王哥与数字（digit）
题面
王哥认为如果一个数从高到低位的数字是单调不增的，那么这个数是有趣的。例如 就是有趣的，而 就不是有趣的。
王哥很快想到了一个问题，求一个区间 内有多少个数是有趣的，但是他觉得这实在是太简单了。于是王哥加强了一下这道题：
给定区间 和一个正整数 ，有 个变量 ，每个变量为整数且在 之间。求在 种不同的变量取值方案中，有多少种取值方案 ，满足 是有趣的。
两种方案不同当且仅当存在一个 使得 在两种方案中的取值不一样。答案对 取模。
。
题解
设 是一个有趣的数，考虑求 的贡献是多少，即有多少种取值方案满足 。先将问题转化为 个范围为 内的变量加起来为 。考虑容斥，钦定有 个变量取值 ，问题变为 个正整数加起来为 ，用插板法可得答案为
所以贡献为：
对于每个 分别计算答案，那么设 ，考虑把原式写成关于 的多项式，即：
于是
再展开：
现在要对于每个 求 ，考虑数位 DP。
设 表示考虑了前 位，最后一位为 ，是否顶着下界，所有有趣的 的 是多少。
那么转移相当于求 ，一项式展开后用 的 次方和乘一个系数来转移即可。
设 ，则复杂度为 ，常数小可以通过。
模拟赛题解/2025.9.15 模拟赛
· 阅读需 5 分钟
T1-Walk
题面
给出一个 的矩阵，起点用 'V' 表示，终点用 'J' 表示，. 代表无敌人，+ 代表有敌人。求从起点到终点的所有路径中，路径上任意点与最近敌人的曼哈顿距离的最小值的最大值。
距离定义为曼哈顿距离：。
。
题解
对于每一个点计算一下距离+的距离，可以用 bfs 实现。
计算两点之间经过点最大值最小的可以用二分答案 + bfs 或者用 dijkstra 来实现。
复杂度 。
T2-Array
题面
给定两个长度为 的数组 ，每次操作可选择 中的一个数，将其变为当前 的异或和。求最少操作次数使 与 完全相同，否则输出 。
。
题解
容易发现这个操作其实就是手里初始有一个数，每次能和其中一个位置交换，最后要 相同
那么我们发现对于每一个联通块需要多操作一次，维护一下构成了几个联通块即可
由于数值范围比较大，需要先离散化一下
复杂度 。
T3-Permutation
题面
给定一棵 节点的无根树，依次以每个节点 为根，求 序的期望逆序对数量（模 ）。
。
题解
首先考虑以 为根的答案， 可以发现， 如果 没有祖先关系， 贡献是 ， 假如 有祖先关系， 是 的祖先， 我们可以通过 dfs 统计 的对数，贡献是 , 即 dfs 的时候维护树状数组，设 为 为根的有根树的子树逆序对数
然后考虑 转移到 （ 的某个孩子），有 对 这棵子树贡献的逆序对数 对除 这棵子树贡献的逆序对数
可以发现， 只有这两个节点的 值会改变， 其他点都不会改变， 因为只有他们变换了父子关系，其他都是兄弟关系
然后我们发现可以维护 对 这棵子树的逆序对(dfs 序+主席树) / 线段树合并
因此我们可以 的从 的答案转移得到 的 值
复杂度 。
T4-Grid
题面
给定 网格，每个点权值 （坐标下标从 ）。选取 个点，定义“坏点”为不满足以下条件的点：
- ，或
- 上一行的左右相邻点 和 （）均被选（若这两个点其中之一不在网格上，则不符合条件）。 一种合法的选点方案当且仅当坏点个数小于等于 。求对于 ，选出的点权值和的最大值，若无合法方案输出 。
。
题解
注意到原图其实被分为了两个图（根据 的奇偶性）
根据观察能发现有一些点不可能被选取
进一步观察原图性质，我们会发现将图进行旋转之后题目限制可以变成要求 和 被选
进一步转化可以发现问题变成每一列上要选取一个前缀，并且当前列前缀高度小于等于右边这一列高度
这个显然可以利用 完成
有一个点可以不符合题目限制将问题复杂化了一些
可以分成三种情况：
- 选一个和当前列已选前缀无关的点（就是在下面）
- 使得当前列高度可以等于右边一列高度 。
- 这一种情况比较容易遗漏，当前列可以在前缀中挖空一段（满足一定条件）
前两种情况相较于原本的 没有什么太大变化
第三种情况需要增加枚举挖空点的上下边界
注意到这样子还是有少考虑
注意做完 后还要考虑上对角线的特殊情况
注意到第三种情况其实不用枚举上下边界
只需要枚举下边界后用前缀和优化
时间复杂度优化到
但这样可能仍无法通过
注意到原图的一些位置是无法选取的，所以在 的时候把这些状态去掉，可以除去很大的常数
模拟赛题解/2025.9.13 模拟赛
· 阅读需 7 分钟
T1-A（a）
题面
一个卖饮料的售货机，价格为 元一瓶，内部已有 枚 元硬币用于找零。 现在你有 张 元纸币和 枚 元硬币。已知售货机每次只能买一瓶饮料，且只 会用硬币进行找零，请求出你最多能买多少瓶饮料。
。
题解
首先答案有上界 。
注意到无论如何交易，纸币与硬币的总数是不变的，所以可以把每次交易看成是分配纸币与硬币给售货机。
不妨设现在购买了 瓶饮料（不超过上界），那么售货机里会有 块钱，在最优策略下就会有 个硬币，此时只要 就一定可以满足。
于是答案即为让上式不满足的最小的 。因为其肯定有一个 的循环节，所以枚举一遍即可。也可以用数学方法做到一个 。
T2-B（b）
题面
我们称一个 的矩阵是好的，当且仅当： • 该矩阵的每一行是 的一个排列 • 定义矩阵转换而来的数字串 是一个长度为 的串，且 现在给定一个好的矩阵 ，求有多少个好的矩阵 满足 的字典序小于 ，答案对 取模。
。
题解
考虑按位从小到大枚举。
假设现在枚举到 ，并且默认 前面与 相同，只在 位置上比 小。设 ，那么根据 是否在 中出现分类，最终都可以规约到如下的“类”错排问题：
已知 个数，用里面的 个数和外面的 个数排列，求错排方案数。
设其方案数为 ，那么就可以用类似错排序列的递推方法求解：
- ，此时就是错排问题；
- ，考虑序列最后一个位置（不在 个数里），那么分类讨论填在这个位置 上的数：
- 填了 个数里面的数，此时有 种
- 填了外面的数，此时有 种
于是就有 。
最后只需要在枚举同一排的时候用树状数组动态维护当前没被用过且出现在 的数的个数。
时间复杂度 。
T3-C（c）
题面
现在有一根数轴，数轴上有 个带编号的点。在时刻 ，编号为 的点在位置 ，有初速度 。保证初始所有点的坐标互不相同。 接下来所有点一起开始运动。如果在时刻 ，编号为 的点向右运动，编号为 的点向左运动碰撞在了一起，把这个碰撞事件记为三元组 ，并令 然后继续运动。注意：在同一时刻 可能有不止一对点发生了碰撞，但是这些碰撞事件相互独立，可以按任意顺序处理碰撞。 把所有碰撞事件的三元组 按字典序从小到大排序。对于给定的 和 ，找到第 个到第 个事件并按顺序输出这些事件的 和 。保证至少有 次碰撞存在。
，，，，。
题解
如果不考虑每个点的编号，一次碰撞可以看作是两个点互相穿过了彼此而不改变方向。所以对于任意时间 ，我们可以知道每个点的坐标。
如果考虑每个点的编号，发现每次碰撞并不会改变带编号的点的相对顺序。
有了上述两个观察，我们可以先进行二分，对于给定的时间 计算出截止到时刻 一共经历了多少次碰撞，从而得到第 次碰撞的时间 。同理得到 。
接下来，我们先计算出在时刻 所有点的坐标。我们知道编号的相对顺序不变，那么就可以按顺序对应出当前每个点的编号。接下来找到所有在时刻 的碰撞。同一个时刻可能存在多个碰撞，但这些碰撞的点互不相同，所以至多存在 个同一时刻的碰撞。时刻 的碰撞次数 ，所以时刻 的所有碰撞总数也是 的。
最后，按顺序模拟这些碰撞，找到对应的三元组并将三元组按给定规则排序，输出对应的区间即可。
时间复杂度为 ，这里 是值域，瓶颈在二分。二分之后的计算可以先排好序然后用双指针加速。复杂度是两个 的小常数程序也有可能通过本题。
T4-D（d）
题面
有一个积性函数 满足如下条件（其中 为质数）： • • • 现在有一个长为 的序列 ，并对其进行 次操作，操作分为如下两种：
- 把 改成
- 查询
请你回答所有查询操作的答案。你可能需要在线回答这些询问。 ：积性函数 拥有如下性质：若 与 互质，则 。
。
题解
考虑 。
然后两部分是独立的，我们可以先求出第一个的乘积，再乘上第二个的乘积。
第一个的乘积其实就是 ，线段树维护即可。
第二部分可以考虑将每个数拆成 的质因子和至多一个 的质因子。
对于 的质因子直接枚举每个质因子，用 修改 查询的分块维护区间该质因子的个数。
对于 的质因子，考虑把所有 的质因子拿出来，设其位置为 ，然后加入若干条线段 ，每条线段的权值为 ，那么只需要求 内部所有线段的权值乘积就行了。用树套树做到两个 ，修改用 动态维护线段。
时间复杂度大概 是 级别的？反正跑不满。
模拟赛题解/2025.9.12 模拟赛
· 阅读需 7 分钟
T1-甲虫（beetle）
题面
小 K 和小 N 带领一群朋友去乘船渡海。最初一共有 个人，第 个人的体力值为 。在岸边有一艘船，这艘船的运行规则如下：
- 每次划船时，船上至少要有 人用于控制船只行驶，同时船上不能承载超过 人。
- 船上所有人必须体力值 才能出发，每使用一次船，船上的人会被运到对岸，此时所有人的体力值减少 （无论往返）。
船可以任意次数往返，你需要判断是否能将所有人运到对岸。
。
题解
注意到一共至少需要往返 次（记为 ），而每个人最多可以往返 次。
因此，只需要所有人的往返次数之和大于 次，就一定能到达对岸。
T2-兔子（bunny）
题面
对于一个长度为 的数组 ，定义一次操作为：选择一个下标 满足 ，一个整数 满足 ，并将 改为 。令 表示对 进行任意次操作后，数组所有元素的按位或的最大值。同时定义序列 的优美度为让数组 的按位或达到 所需的最小操作次数。
现在有一个数组 ，同时小 K 会给你 个询问，每次询问给定 ，求 构成的子数组的优美度大小，请你回答这个问题。
。
题解
令区间 或值最高位为 ，那么最大值为 ，可以对区间任意一个 的数，操作两次 得到。说明操作次数只有 ， 是容易的，重点在于判断 。令或值最低/最高为 的位为 ，那么能操作的数必须满足 位为 ，值要 。可以存储 棵线段树，第 棵存每个数 位第一个 的位置，这样只要区间查询第 棵线段树的区间极值是否 。
有可能操作完一个数之后，除了 之外的某些位变成 了。但这样的数最多只有 个，拎出来单独判断，并对其他 个区间正常 check。
时间复杂度 。
T3-狼（wolf）
题面
C 城正在举行一场盛大的运动会，小 K 和小 Y 作为长跑项目的志愿者，负责记录数据。比赛共进行 轮，有 人参加。第 轮比赛结束后，小 K 和小 Y 会按照以下规则在大小为 的表格 中记录成绩：令第 个到达终点的运动员编号为 ，编号为 的运动员的排名为 ，那么 。
但赛后小 Y 不慎丢失了表格，幸运的是小 K 记住了 个大小为 的可重集 ，其中 表示表格第 列的所有元素。请根据小 K 的记忆，还原出任意一个满足记录规则的表格，或者报告无解。
题解
观察到如果存在 ，那么必然有 ，且两两对应。于是我们建立一张 个 点的图，将 和 里所有元素连有向边。最后 和 的边数如果不相等则无解，否则我们构造证明有解。
把 和 看成一组匹配，等价于我们图中需要找到 组匹配。每个点的度数为 ，跑一遍欧拉回路之后，每条定向后的边 ，看成一张新图上左部点 向右部点 的边。
新图用 Hall 定理易证明存在合法匹配，暴力跑网络流是 的，但是因为这是 - 正则二分图，所以单次匹配可以做到 （link），总时间复杂度 。
但实际测出来根号和 并没有明显的效率差异，所以最后一档只给了 12 分，普通流卡卡常或者换种写法大概也是可以过的。
T4-浣熊（raccoon）
题面
小 H 准备为小 K 写一句拼贴诗，诗句均由小写字母组成。现在小 H 手上有两句相同的诗句 。他希望取出 的一个前缀 和 的一个后缀 （ 均可以 为空），并把他们拼接成一句新的诗 送给小 K。
但并不是每一种组合都是优美的。小 K 有一个喜欢的词 ，如果 存在一个子串为 ，那么 是优美的。请帮助小 H 统计有多少本质不同的拼贴诗 ，且其是优美的。
定义两句诗 本质不同当且仅当 或者存在 且 。
。
题解
令 ，。考虑一个弱化的问题：。此时仅要考虑 本质不同。
对于一个方案 ，只统计 的情况即可做到不重复计数（一个 只被 最大的方案计算到）。回头看包含 的条件，容斥掉 在 或者 出现的情况，剩下 跨越匹配的出现次数。枚举在原串中开始匹配 的位置 。
令 表示从 开始能匹配 的最长长度，那么最终 必须为 ， 否则要么不合法，要么不满足起始条件 。于是我们只需要找到多少个后缀开头能匹配 ，这个可以通过一遍 函数解决。
最后有个问题是相同的 可能会匹配多个跨越的 。处理方法是前面枚举 的时候钦定其为第一个匹配的开头，容易发现条件是不存在 和 的 ，使得 。
对串 建立失配树并打标记即可，注意一些边界的细节，总时间复杂度 。
模拟赛题解/2025.9.11 模拟赛
· 阅读需 8 分钟
T1-买宝珠（pearl）
题面
鲁国突然从齐的侧翼发动反击，早已被锁链连接的齐国战车这时无法灵活的转过来应敌。于是，齐军一击即溃，只能丢盔弃甲，仓皇而逃。
在逃跑过程中，鲍叔牙竟然弄丢了管仲代购的鲁国特产。
已知鲁国特产是由 条丝带连接 个宝珠构成的。即你可以将鲁国特产看成一棵树。
树的每条边上的颜色都是 种颜色中的一种。如果树上的一条路径是彩色的，意味着这条路径上至少包含两种不同颜色的边。
鲍叔牙还记得 条彩色路径的起点和终点。他现在想知道满足条件的树有多少可能？
由于答案可能很大，所以请将答案对 取模。
。
题解
考虑暴力枚举每个人的决策，同时维护在前 轮决策下，当前的 集合，如果 ，那么立刻返回 。时间复杂度是 的，因为每次决策都会把 分成两个不交的集合，每个元素都只会向一侧递归，一共递归 层。
考虑对于先手来说，每次进行决策，如果他选择集合大小更小的那一侧，那么每次操作集合大小减半，需要 次操作就可以使答案为 ，那么当 的时候，答案不可能大于 。同理答案不可能小于 ，因此答案一定是 。
时间复杂度 。
T2-玩游戏（game）
题面
小 X 和小 Y 是好朋友，有一天他们在玩游戏，规则是：
- 小 X 先手，小 Y 后手，轮流进行操作，共有 轮操作，有一个集合初始为 。
- 第 轮操作有一个参数 ，当前轮的操作者有以下两个选择：保留 中所有是 倍数的数字，或者保留 中所有不是 倍数的数字。
- 进行了 轮操作后两人获得的权值是 中的数字之和， 可以为空。
小 X 希望权值最小，小 Y 希望权值最大，假设他们足够聪明，那么游戏最终的权值是多少。 。
题解
考虑不合法的方案。
如果 ，这样算会重复计算多条路径同时不合法的方案，我们发现 ，于是可以直接暴力枚举容斥。
具体来说，就是枚举不合法路径的集合 ，对于每条路径，把它所有边合并到某一条边上（如果路径有相交，当然是合并成一条边了）。然后统计合并后的边数 ，当 为偶数，让答案加上 ，当 为奇数，让答案减去 ，枚举路径集合可以直接状态压缩，合并可以用并查集实现。
时间复杂度为 。
T3-游乐场（playground）
题面
有 个人来游乐场玩水上飞人，第 个人想玩至少 次，每次水上飞人恰好有两个人游玩，并且为了防止无聊，两个人 至多一块玩一次水上飞人。每个人有一个勇气值 ，如果他的勇气值大于等于所有和他一块玩过水上飞人的人，那么他会收获 的快乐值；如果他的勇气值小于等于所有和他一块玩过水上飞人的人，那么他会收获 的快乐值。但如果他的勇气值恰好等于所有和他一块玩过水上飞人的人（或者没有和任何人玩过水上飞人），他并不能获得 的快乐值，而是只能获得 的快乐值。并且如果他的勇气值既不同时大于等于也不同时小于等于所有和他一起玩过的人，他就会生气并把游乐场炸掉。除此以外，如果有人没玩够 次水上飞人，或者有两个人 一块玩了至少两次水上飞人，游乐场也会被炸掉。
作为游乐场的管理员，你要规划若干次水上飞人，使得游乐场不会被炸掉，并且所有人的快乐值之和最大，如果无解输出 。
，，，。
题解
我们可以把题意改写：给每个人钦定他是大还是小，然后再判断每个人是否合法。对于一个人 ，设勇气值小于他的人的个数为 ，其中选大的人的个数是 ；勇气值大于他的人的个数为 ，其中选小的人的个数是 ；勇气值等于他的人的个数是 ，判句是：若 选大，则 ；若 选小，则 。
先处理勇气值互不相同的情况。考虑按勇气值从小到大考虑人，那么记录一下当前有多少个人选大以及前面选小的人限制后面最多选几个小就能判断然后转移了。具体来说设 状态 表示考虑完前 人，选了 个大的， 及以后最多选 个小的，那么转移为：
暴力做复杂度 。
如果有相同的，那就不能直接以某一个顺序依次转移每个人。考虑把勇气值相同的人一块考虑，那么状态 改为表示考虑完 的 ，选了 个大的， 的 中最多选 个小的，对于每一组勇气值相同的人我们只用知道选了几个大以及选小的内部最紧的限制即可像之前一样转移，但暴力实现复杂度最劣 。考虑把第二种转移里的取 改成分类讨论，如果是 则只需要知道 的 ；如果是 （ 为选的小的个数），考虑维护一个转移数组 ，即 的最大系数 ，不难发现原来的转移相当于让 这一维上的一个前缀的系数对一个数取 。使用后缀优化即可做到 。
T4-子矩阵（matrix）
题面
你要维护一个 的矩阵 ，其中第 行第 列的元素记作 。行和列从 开始标号。初始时这个 的矩阵是全为 的 矩形。
你需要支持 个操作，每个操作都是将一个从 到 的矩形反转，矩形反转即将矩阵中的元素 变 或者 变 。
你需要在所有操作结束之后，对最后的矩形求出有多少个子矩形，子矩阵要求：非空且连续，第一列全为 或者最后一列全为 。
答案对 取模。
，，。
题解
考虑从左往右扫，使用支持区间反转的数据结构（平衡树）维护珂朵莉树，中间 翻转，左右两边 或者 。
考虑对于 中的维护的一个区间，自诞生之日起它可能当过 也当过 ，然后记录—下它当过多少次 记为 ，考虑它对答案的贡献。
因为我们要的是对于 个区间，每个区间求出 列中有多少列全为 ，容易发现上面的一个区间 会对 的 都产生 的贡献。考虑这个东西在被破开连续段之前贡献只有两种，即取反和不取反，通过颜色段均摊之后我们可以拆成 个这样的 ，求出每一个区间 后扫描线 + 线段树维护即可。
复杂度 。
模拟赛题解/2025.9.9 模拟赛
· 阅读需 4 分钟
T1-图（graph）
题面
给定一个含有 个节点和 条边的有向图，每个节点恰有两条出边和两条入边。
删去 条边，使每个节点恰好还有 条入边和 条出边。
求删边的方案数，对 取模。
。
题解
首先，原题的条件可以转化为每条边的两条出边不能同时删除，入边不能同时删除。
将边转化为点，在互斥的两条边之间连边，则原题条件就被转化为了求图上的最大独立集。
因为新图中只有偶环，所以可以直接将答案表示为 ，并查集维护即可。
T2-树（tree）
题面
有一棵 个节点的树，每条边的边权为 。
你要从 走到 ，一开始有体力 ，每次经过一条边 体力就会减少 。
如果体力变得不超过零，则会将体力恢复到 。
问最后一共会恢复几次。
。
题解
可以使用树链剖分+链上倍增的方法，复杂度 ，但有 风险。
容易发现如果只考虑朝上走，就是求出每个点可以走到的点，接下来就是一个简单的倍增。
接下来考虑往下走的一段。这里有一个神秘的观察，对于一条链，如果体力都是满的从两边开始走，那么复活的次数是一样的。
考虑组合意义：这个等价于将整条序列分成尽量少的段，使得每一段之和都 ，所以从两边开始贪心都是对的。
所以可以找到拐下去的点之后，从下往上倍增。
T3-团（clique）
题面
给定无向图 ，。
对每个顶点 给定权值 。
边 当且仅当 。
求 的最大团的顶点数。
。
题解
观察到题面实际上就是两点之间的曼哈顿距离，显然不好维护，可以转化成切比雪夫距离。
因此题面就转化为在平面直角坐标系中一个边长为 的正方形最多能覆盖多少个点。
可以用扫描线维护，复杂度 。
T4-序列（sequence）
题面
有一个序列 。记 为前缀最大值。
定义一个序列是好的当且仅当：
- 。
- 。
对于 的所有数，求在所有好的序列中出现次数的平方总和是多少，对 取模。
。
题解
首先可以把平方看成可重复地选择两个数字，那么对于 ，考虑 表示前 个数，当前最大值为 ，选了多少次的方案。
转移可以选择每次要不要增大 ，并且选择几次，当 和 时，考虑两种不同的转移，直接 的复杂度为 。
当 不同时，可以发现前后两种情况的转移是分别相同的，即只有变化点不同。
考虑预处理前缀和后缀的转移，然后枚举断点，将前后方案数相乘即可。
模拟赛题解/2025.9.8 模拟赛
· 阅读需 6 分钟
T1-入门题（basic）
题面
对于一个长度为 的序列 ，我们称其是 序列当且仅当对于每一个 ，都满足 。
给定一个长度为 的序列 ，求其有多少个非空子序列是 序列，答案对 取模。
。
题解
注意到实际上一个点 要出现在子序列中，加入前的 只有 三种可能性。
于是设计状态 表示 时，满足条件的非空子序列数量。
然后注意到从 转移只可能出现一次，且之后只能从 转移。
所以将状态更改为 表示是否已经出现过该转移，转移式是显然的。
复杂度 。
T2-人门题（basis）
题面
给定一个长度为 的序列 ，以及一个长度为 的序列 。
定义一次操作过程如下：
- 选择集合 。
- 对于每个 ，令 。
问最少需要多少次操作才能使序列 变为单调不降的序列，若无解输出 。
。
题解
发现答案是最小化最大操作次数，考虑二分答案。考虑如何判断一个 是否可以作为答案。
有一个显然的贪心策略，直接求出每个位置可以在 步内变成哪些值，然后每次取出这些值里面比上一个位置大的最小值作为这个位置修改后的值，然后继续检查下一个位置。
考虑稍稍修改一下这个贪心，即我记一个指针表示当前这个位置至少要达到多少，若可以在 步内达到，则继续检查下一个位置，若不可以，则指针的值加一，然后继续检查。
预处理一下即可做到 回答单个 ，于是总复杂度 。
T3-
题面
给定一个长度为 的序列 。
定义一次操作过程为选择一个位置 ，令 。
有 次询问，每次给出一个区间 ，问至少需要多少次操作才能使得区间 成为整个序列唯一的最大子段和。
如果无论如何操作， 都不可能成为整个序列唯一的最大子段和，输出 。
由于我们认为不选子区间是一种和为 的方案，所以要求唯一的最大子段和最后是大于 的。
。
题解
考虑无解情况。
无解时，一定存在除去 区间后一个前缀区间的后缀或一个后缀区间的前缀满足区间和为正数。
直接用线段树维护 和 的最大前/后缀即可。
记 为原序列的最大子段和。
考虑区间内部，若存在一个区间 满足 ，并且 ，则需要首尾各额外 ，防止内部出现其他区间满足最大子段和，不满足唯一性。
如果外部有其他的区间，则额外 ， 满足唯一性。
复杂度 。
T4-
题面
定义作用于 上的满足结合律的运算 满足 。
给定 个限制，每个形如 。
定义一个元素 为交换子，当且仅当 。
对于每一个满足条件的运算 ，记其交换子的数量为 。求所有满足条件的 运算所对应的 的和，对 取模。
。
题解
令 ，定义如下二元关系：
- 表示 。
- 表示 。
- 表示 或 。
- 表示 或 。
引理 1. 是一个等价关系。进一步地， 划分出的每个等价类 中，要么 ，要么 。
证明. 自反性和对称性显然，下面验证传递性。设 。不妨设 。
- 若 ，则 ，同理 ，因此 。
- 若 ，类似地可以证明 。
- 若 ，则 ，但另一方向， 无 论 是 还是 ，最终都得到 ，矛盾。
- 若 ，则 ，矛盾。
注记 1. 。因此 可以被投影到 上。
引理 2. 是偏序，且 上， 定义了一个全序。
证明. 证明预序。自反性显然，考虑传递性。设 。
- 若 ，则在 中已被证明。
- 若 （换言之，）：
– 若 。
– 若 。
- 若 ：
– 若 。
– 若 。
- 若 ，则 。 证明 是序关系后，全序显然。
于是我们直接 即可，枚举每次加入的等价类，复杂度 ，然后用 优化 一下即可做到 。
模拟赛题解/2025.9.5 模拟赛
· 阅读需 9 分钟
T1-异或和（xorsum）
题面
给定 ，求有多少个 满足：存在两个非负整数 使得 ，且 ，其中 表示 进制不进位加法。
具体来说，若 在 进制下从低到高第 位分别为 ，则 在 进制下从低到高第 位为 。
你需要回答 次询问。为了减少输出量，记第 次询问的答案为 ，你只需要输出
。
题解
法一：数位 dp
先考虑二进制的情况， 即异或。
若 ，则对于 二进制下为 的那些位， 在这一位上必然有一个 和一个 ，对于 二进制下为 的那些位， 在这一位上可以有两个 或两个 。因此记 ，即 ，要求 的第 位若为 ，则 的第 位必须为 。
或者说容易发现 ，所以 ，显然若 某位为 则 这一位必须为 。
可以对着这个条件数位 dp，复杂度 ，常数较大，期望获得 30~70 分。
对于 的情况，条件是类似的，但是在数位 dp 时无法直接枚举 这一位填什么。但是容易根据进位情况唯一确定 ，因此仍然可以数位 dp，复杂度 ，期望获得 40~100 分。
法二：递推
考虑 的部分分，如何获得一个快速递推答案的式子。
记 为 的答案，打表或许可以发现 。 证明是简单的，显然若 ，则 最低位必然一个 一个 ， 最低位必然为 ，所以可以简单地把最低位删除，递归到 。
若 ，则 最低位可以两个 或两个 ， 最低位必然为 ，因此删除最低位后可以选择递归到 或 。显然 和 奇偶性不同，所以不会算重。
复杂度 ，期望获得 30 分。
若 ，可以类似地得到 。
复杂度 ，期望获得 40 分。
根据递推式，如果想求出两个相邻的 ，则只需要求出两个更小的相邻的 即可。复杂度 ， 期望获得 100 分。
T2-图计数（gracnt）
题面
给定一张 个点 条边的无向图（可能存在重边自环），第 条边连接点 和 ，有一个权值 和一个初始为 的计数器 。
你可以任选一个起点，沿着图上的边走任意多步，每次经过第 条边时，会将 改为 。
求这个过程可以生成多少种不同的 ，对 取模。
。
题解
显然两个连通块之间是独立的，记第 个连通块的答案为 ，则最终答案为 （注意避免算重 全为 的情况）。接下来只需考虑连通图。
记 为第 条边的实际经过次数，这样一组 是否合法实际上就是个欧拉路问题，结论是只保留 的边后，图仍然连通，并且只存在至多两个度数为奇数的点。
显然 可以任取 ，所以只需将 加上 ，就不会改变度数奇偶性，并且无需考虑图连通的限制。
如果 是奇数，那么无论 是多少，都可以通过加上一个 改变 的奇偶性，所以此时 取什么实际上是无所谓的，只需将答案乘上 即可。可以通过 的部分分。
如果 是偶数，则 的奇偶性与 相同，我们只关注奇偶性，因此可以先将答案乘上 。
先考虑 的情况。不妨先提取出连通块的一棵生成树，可以说明，任意指定零个或两个度数为奇 数的点，并任意指定非树边的 ，都唯一存在一组树边的 使得度数合法。证明也很简单，树的叶子节点可以唯一确定与其相连的边的状态，这样每次剥掉一层叶子即可。
因此，对于一个 的连通块，如果有 个点 条边，答案为 。可以通过 的部分分。
接下来考虑一个连通块 既有奇数也有偶数的情况。对于一条 为奇数的边，可以同时改变连接的两个点的度数奇偶性，可以理解为度数可以沿 为奇数的边传递。因此直接将 为奇数的边连接的两个点合并起来即可。
整体算法流程是：将 为奇数的边缩起来之后，对于每个连通块，统计点数和边数并计算答案。可以 dfs 或者并查集维护。
复杂度 。
T3-黑白灰（blwhgr）
题面
数轴上有黑/白/灰三种颜色的点，每种各 个。第 个黑/白/灰点的坐标为 ，第 个灰点有权值 。
你可以执行任意次操作，每次操作你可以选择三种颜色的点各一个，记你选择的黑/白/灰点的坐标为 ，满足 ，然后将这三个点删除，并得到你选择的灰点的权值。
求你能得到的最大权值和。
。
题解
特殊性质都有简单的贪心方式。
可以建出费用流模型：将灰点拆为入点和出点，源点向黑点连边 ，黑点向后面的灰点入点连边 ，灰点入点和出点之间连边 ，灰点出点向后面的白点连边 ，白点向汇点连边 。 跑最大费用流即可。
依据建边方式可以通过 或 的部分分。
根据费用流模型可以得到结论：记进行 次操作的最大答案为 ， 有凸性，因此是单峰的。可以三分操作次数，问题转变为求进行 次操作的最大答案。
显然黑点一定选前 个，白点一定选后 个。考虑黑白点之间的匹配，如果存在交叉，即黑点 ，白点 满足 匹配 且 匹配 ，且 ，交换匹配关系一定不劣。所以可以认为从前往后第 个黑点匹配第 个白点。
考虑权值最大的灰点，如果不被任何一组黑白点的匹配覆盖，那么可以直接扔掉不管，否则这个灰点一定会被某次操作选中。证明考虑如果这个点没有被选中，直接将某个覆盖其的黑白匹配选择的灰点修改为这个点即可使答案增加。
这个权值最大的灰点直接贪心选择其左侧第一个黑点和右侧第一个白点即可。注意这可能会破坏我们既定的黑白匹配关系，但是不重要，将黑白点重新按顺序匹配即可。
这样就可以按权值从大到小依次考虑每个灰点并计算答案。容易使用 multiset 或并查集，树状数组等数据结构维护，单次三分复杂度 ，总复杂度 。
T4-斗恶龙（dragon）
题面
有 个恶龙，第 个恶龙初始等级为 。你要支持 次操作：
-
1 l r k，将第 个恶龙中所有等级为 的恶龙的等级改为 。 -
2 l r k，将第 个恶龙中所有等级为 的恶龙的等级改为 。 -
3 l r x y，求第 个恶龙中有多少恶龙等级在 之间。
。
题解
如果没有修改，查询是普通二维数点，可以维护一棵主席树，版本 维护了所有等级 的点。
对于修改 1 l r x，将版本 的区间 直接替换为版本 的即可。对于修改 2 l r x，将版本 的区间 直接替换为版本 的即可。
复杂度 。
对于特殊性质都存在较为简单的维护方法。也有一些根号做法。
模拟赛题解/2025.9.4 模拟赛
· 阅读需 5 分钟
T1-空洞骑士（bit）
题面
多组询问，每组询问给定一对正整数 ，在闭区间 内所有整数中，找到二进制表示中 个数最少的数。如果有多个这样的数，找到其中最小的那一个。
。
题解
考虑直接按位贪心求解。
从最高位开始，在保证 的情况下，尽量在高位放 ，并且得到的值一旦 就跳出。
此时可以保证最终得到的数可以保证在 区间内，并且 的数量最少。
再考虑如何求出最小值。
从最高位开始枚举，显然尽量要将 往低位放，故除非后续位数全部在最高位放 直到放完也 ，否则不放，显然一定最优。
复杂度 。
T2-丝之歌（infected）
题面
有一棵 个节点的树，选择两个节点将树切断，得到三个连通块。
设三个连通块的大小分别为 ，求出 的最小值。
。
题解
三个连通块不好求解，考虑固定其中一个连通块的断点。
此时显然使另外两个连通块大小尽量接近最优，因此我们将所有点的子树大小（记为 ）存入 二分求解。
然而当另一个断点是当前断点祖先时，其 包含当前点的 ，所以我们开两个 ，分别存储祖先节点和非祖先节点，祖先节点更新答案时减去当前节点的 即可。
复杂度 。
T3-即将于今晚（skill）
题面
有编号为 的三个值，初始时都为 。
可以用 次操作对值进行修改，每次操作为：
- 选择其中一个值，设选择的值为 ，使其值增加 。
- 对于另外两个值，如果已经有 次没有进行操作，则使其值减少 。
- 三个值都不会小于 ，会始终和 取 。
求在 次操作结束后，三个值之和的最小值。
- 。
- 。
题解
我们注意到两个性质：
- 如果一个值被修改过，那么将它重新修改到 显然不优（可以将修改它的操作变为修改其他值）。
- 对于一个数，它修改后最多被搁置的轮数是 级别的，因为被搁置 轮后产生的减值是 ，而值不会被减到 。
因此我们可以设计状态为 ，表示进行到第 次操作时，本次操作选择的是第 个值，下一个值被搁置了 轮，下下个值被搁置了 轮。
每个状态向下一个状态的转移显然只有三种可能：
- 仍选择当前点。
- 选择下一个点。
- 选择下下一个点。
此时的转移是显然的。
注意：一个点没有被修改过之前不会产生减法，所以如果 或 为 ，其转移方向应该为 。
最后我们注意到 状态只会从 转移过来，所以采用滚动数组。
复杂度 。
T4-十点发售（orandgcd）
题面
给序列 ，，。
定义区间 的价值为 按位与， 按位或， 的最大公因数，这三者的乘积。
次查询，每次查询给出区间 ，查询满足 的 的价值之和。
结果对 取模。
。
题解
考虑扫描线，扫到 时维护 表示区间 对应运算的答案， 表示左端点在 内，右端点在 内的区间的权值和（相当于 的历史和，虽然这道题并不需要用到历史和），那么询问 的答案可以拆分为扫到 时的 。
一个并不是很显然的结论是：扫描线 ， 的值只有一段 会 改变，然后这个 的大小是均摊 的。具体证明可以考虑拆位，每一位会在什 么时候改变这个乘积。
于是我们就可以维护 这个数组了，对于 这一段的 没有发生改变，但是 改变了，直接历史和复杂度又太巨大了，可以考虑将 的定义式改为 ，这样只要前缀 不改变， 也不用修改，需要求值的时候算一下就行。
总复杂度 。另外本题有一个数据不变，时限 3s->1s 的版本（P9335）。
模拟赛题解/2025.9.3 模拟赛
· 阅读需 9 分钟
T1-那头与出题（data）
题面
那头在出题时发现他不会写一道题的 generator，需要你进行帮助。
我们称一个对无限大网格图的黑白染色方案是合法的当且仅当所有黑色点四联通，所有白色点也四联通。
具体的，我们在 与 之间连边当且仅当 且两个点颜色相同，如果得到的图的联通块数为 或 ，那么染色方案合法，否则不合法。
初始时所有点都是白色的，你需要维护 次修改。
第 次修改有两个参数 表示尝试把 涂黑（保证这个点当前是白色)。如果涂黑后染色依然合法则执行该操作，否则放弃该操作。
你需要求出每次操作是否被执行。
。
题解
每次新加入的点是否能让黑色保持联通是易于判断的，判断新加入的黑点上下左右是否有其他黑点即可。
考虑如何判定白色能否保持联通，注意到只需要考虑新加入点周围 九宫格内的情况即可，九宫格外的白点并不会受到影响。
因此每次检查新加入一个点后九宫格内黑色白色的连通性即可。
T2-那头与分值（score）
题面
那头需要完成 道题目，第 道题目难度为 。那头有一个智慧值 ，他完成所有题目需要 的时间。
那头会 次调整自己的智慧值，你需要每次告诉他完成所有题目会完成的时间。即给定 ，你需要求出 的值。那头不希望等待，所以本题部分测试点要求强制在线。
。
题解
考虑决策答案每一位是 还是 。对于第 位，需要查询有多少个 满足 的第 位为 。可以转化为统计进位次数。这相当于查询 在一个区间内的值的个数， 可以预处理 并对 排序然后二分查询。
复杂度 ， 期望得分 分。
尝试优化以上算法。预处理部分容易优化，可以通过归并做到 （但这部分 不是瓶颈，不优化也可以通过）。难点在于优化询问。如果允许离线，可以对于每个 也预处理 并排序，然后双指针扫描回答询问，复杂度 ，期望得分 分。
如果要求强制在线，我们无法对 排序预处理，所以只能尝试通过本次询问第 位 的结果推出 位的结果。考虑一次询问是要求 的最大的 的位置。当 ，式子左侧的值要么不变，要么增加 。这启发我们预处理 ， 辅助转移。如果可以得到以上数组，每次 可以直接通过调用 完成。 可以和 一起在归并时求出。
复杂度 ，期望得分 分。
T3-那头与观测（observation）
题面
那头住在一棵 个点的树上。
那头在树的每个节点上都放置了一个头。其中 号节点上的头为 号头，其高度为 。对于整数 ，称两个不同的头在视线高度为 时可以互相望见当且仅当：
- 两个头的高度都 。
- 两个头所在节点的简单路径上没有其他头或其他头的高度都 。
对于每个整数 ，求有多少个有序三元组 满足：
- 互不相同。
- 在视线高度为 时， 号头和 号头可以互相望见且 号头和 号头可以互相望见。
。
题解
考虑按编号从小到大删点。时刻维护一个 个点的无向图 。 中 有边当且仅当 在视线高度为 时可以互相望见。令 在 中的度数为 ，则答案为 。
直接建边边数过多，且维护图并不方便。考虑建一些虚点让图变成一棵树。删点开始前，对于原树上的一条边 ，在新树上连接 和 。设编号 的为白点， 的为黑点。删除 相当于把 的子白点与它的父白点合并，可以使用并查集维 护。容易发现新树上的点是黑白相间的，且对于 中的边 ，新树上一定存在恰好一个白点 满足 这两条边在新树上存在。为了方便，以 作为新树的根，这样根一定不会被删掉。
考虑如何算答案。把三元组 变成 （ 是白点）。令 为白点 的 黑儿子个数，分情况讨论：
- 当 时，相当于在 的邻点中选 ， 的邻点有 个（因为要算上他的 父亲）。故对答案的贡献为 ，其中 为白点点集。
- 当 且 为 的儿子时，相当于分别在 的儿子中选 ，贡献为 。 即 。其中 为 的儿子集合， 为黑点点集。
- 当 为 父亲， 为 儿子时，相当于在 的邻点中选 ，在 的儿子中选 ， 中选 。答案为 。乘二是因为三元组是有序的， 应该被算两遍。
每次删除一个点会影响其下一级儿子与上三级父亲。因此对于一个白点维护其下一级， 下三级信息，对于一个黑点维护其下两级信息即可。具体地，可以令 ，。删除 的复杂度为并查集的复杂度加上遍历 的儿子的复杂度。
T4-那头与方程（equation）
题面
给定正整数 。
请判断是否存在非负整数 ，使得对于所有 ，都有 。如果存在，请输出所有满足条件的 中最小的一个对 取模的结果；如果不存在，请输出 。
。
题解
先考虑 的情况。
将式子两端同乘 ，得到 。
此时题目条件为 ，其中 。
即找到一个最小的 使得 ，则此时 。
我们尝试将 的质因子筛出来。 若 ，则存在 ，则 。
若 ，则根据 显然有 ，与条件 矛盾。
所以 ，即每个 仅存在 的质因子，以及有可能含有唯一的 的质因子。
对于 的质因子 ，我们只需找到最小的 使得 （这个可以 ），然后任意满足 的 一定可以表示为 。
求出了 的质因子表示后，因为有 ，我们就可以枚举 来试了。这里需要分讨 的大小以及 的正负性，具体可详见 std。
最后的问题是， 怎么办？令 ，容易发现 ，这是判断是否有解的充要条件。
然后可以求得子问题 ，最终答案为 。
模拟赛题解/2025.9.2 模拟赛
· 阅读需 8 分钟
T1-删树游戏（game）
题面
有一棵由编号为 的 个节点构成的有根树，其中 为根节点， 号点的父亲为 。此外，每个节点都有一个互不相同的整数权值， 号节点的权值为 。保证 为 的一个排列。
我们从 出发，每次移动到当前节点的子节点中权值最小的一个。如此重复，直到到达某个叶子节点。这样得到的路径记作 ，我们称其为特殊路径。
定义一次删除操作如下：
- 设当前树的特殊路径为 。
- 令 从 到 ，依次执行：交换 与 。
- 删除树中 与其父亲相连的边。
我们对这棵树进行 次删除操作，你需要在每次操作前求出 号点的权值 。
。
题解
定义删除序列 ， 为这一棵树第 操作前根节点的权值。
对于一个点 ，设它操作选中了子节点 多次，那么 的变化一定形如 子树的删除序列。
那么求 子树的操作序列相当于先加入 ，然后把子节点的删除序列归并起来。
注意到这个删除序列就是 子树的一个 BFS 序，而且我们要最小化这个 BFS 序的权值的字典序。
用堆维护 BFS 即可。每次取出最小权值点后加入所有的子节点。
复杂度 。
T2-身份猜测（identity）
题面
这是一道交互题。
现有 个人，编号为 。其中恰有 个人是诚实的， 个人是不诚实的。每个人都清楚所有人的身份，但你知道的仅有 和 的值。你需要去确定每个人的身份。
如果你在已知 的情况下无法通过询问确定所有人的身份，则报告不可能。
否则，你可以进行不超过 次询问。每次给定 和 ，向 询问 的身份，交互库返回规则如下：
- 如果 是诚实的，那么 会如实返回 的身份。
- 如果 是不诚实的， 会任意选择回答。注意 可以按照某种策略回答。
交互库会通过你的询问次数评分。
- 如果你未能正确判断有无解，或交互过程不合法，得 分。
- 如果无解，得 分。
- 否则，如果你返回的身份不正确，得 分。
- 否则，你的得分由查询次数 决定：
| q | 得分 |
|---|---|
| 40 | |
| 55 | |
| 65 | |
| 85 | |
| 100 |
且 。
题解
一个观察是，我们能分辨身份当且仅当 。
如果 ，那么我们可以从 个假的人中选出 个人，对这 个人询问时按照这 个人为真，其他都为假来回答。然后就无法判断这 个人是真是假。
如果 ，那么对于每个人 ，我们询问其他所有人对他的评价。如果有 个人认为他是真的，那 么就是真的，否则即为假。注意到我们可以认为 声称 是真的，那么只要做 次。
考虑去找一个真的人，然后再通过他问出所有人的身份。
因为 ，考虑类似摩尔投票的思路。
如果 认为 是假的，那么 和 中有至少一个为假，可以直接删除。
否则，如果 和 都认为对面是真的，那么 和 的种类相同。
于是有一个 次的做法：
- 我们维护集合 ，满足 中的人的种类相同。加入一个人 时，讨论和集合中任意一个人 的关系。
- 如果 认为 假或 认为 假，那么可以直接删除 和 。
- 如果 和 都认为对面是真的，那么就把 加入 。
考虑优化。我们不需要维护一个身份相同的集合，而是维护一条链 ，满足 认为 是真的。
实际上， 的真实身份一定是一段前缀是假的，剩下一段后缀是真的。
那么每次我们加入 时，只要看 是否认为 是真的。如果是，则加入 ，否则删除 和 。
因为 ，而我们每次删除的 和 中至少有一个是假的，因此最终的 一定包含真人，即 一 定为真。
那么我们再拿 把所有人问一遍即可。询问次数 。
T3-序列计数（count）
题面
给定一个长度为 的自然数序列 ，满足 。
序列还需满足 条限制。
第 条限制为 。
请输出合法的序列 的个数，对 取模。
题解
对于第 个限制，它首先约束了 都是不超过 的。
记 为 的上界。这个可以直接并查集预处理。
考虑对值域扫描。
对于一个 ，我们在处理 的限制时， 的点都是不用管的。因为它们不可能成为一个区间的 。因此我们可以取出所有 的点和 的限制。
那么这时限制就变成一个区间必须包含至少一个 的点。
考虑 表示 ，此时 之前的点方案数。
那么下一个 的点 需要满足不存在区间满足 ，这样的 形如一段前缀，可以差分解决。
时间复杂度 。
T4-树上查询（tree）
题面
有一棵由编号为 的 个节点构成的有根树，边有边权。 为根节点，节点 的父亲为 。对于 ， 与 之间的边权为 。
定义 为 子树内经过 的最长链长度。
进行 次操作，每次将一条边的边权加上一个正整数。
在第一次操作前和每次操作后，输出
-
。
-
时 。
-
每次操作 。
题解
是 子树内以 为端点的最长链和与最长链无公共边的次长链之和。
对于每一个点 ，我们记录 为子树内与 距离最大值和次大值。这里次大值到 的链需要 和最大值的无公共边。
考虑动态维护长链剖分，那么子树的 就是实链上儿子的 ，次长链 就是虚儿子的 的最大值。
对于一次修改 ，我们先对 子树内的 和 整体加 。
然后找到 子树内最大的深度，对于 的所有祖先去更新。它对于长剖的影响是把 到根链上一段后缀 变成实链。
这个是和 LCT access 类似的，一个结论是虚实边变化次数是 的。证明考虑轻重链剖分，这 个就是在 dfs 序上颜色段均摊。
那么考虑去数据结构统一维护实边，暴力修改虚边。
一条实链，操作相当于对一条链的 加上 。
对于一条虚边，操作相当于对于单点查询 和 ，然后进行单点改。
于是我们需要支持：
- 子树加，查子树最大深度。
- 对于 子树加、链加，查单点。
- 对于 子树加，查单点。
- 动态修改一个点是否是实儿子。
- 查询一个点所在长链顶点。
第一条线段树维护，第二三条可以树状数组维护。
第四五条 std 用了倍增树状数组维护，复杂度 。常数较小，可以通过。
实际上也可以用一些办法去掉一个 ，做到 。
模拟赛题解/2025.9.1 模拟赛
· 阅读需 9 分钟
T1-序（ryvius）
题面
对于一个长度为 的正整数数列 ， 是好的当且仅当对任意 。
现在有一个好的数列 ，可以对这个数列执行以下操作：
- 选择一个位置 和一个正整数 ，将 变为 ，需要保证每次操作后这个序列都是好的。
要让整个序列操作完之后只有两种不同的数值，求至少要操作多少次。
。
题解
考虑到序列的最终形态是两个数 交替出现，于是将序列按位分为奇偶两部分。
考虑对于两个数，将序列调整到对应状态的最小次数，显然由两个部分组成：
- 序列中不满足最终形态的数的数量
- 存在这两个数相邻的情况数量
于是考虑枚举偶数位并统计奇数位贡献，对于不存在第二种情况的数对，可以直接选择出现次数最多的奇数位，显然此时结果最小。
对于存在第二种情况的数对，因为这样的数对显然不超过 个，因此可以用 map 维护，直接枚举。
复杂度 。
T2-破（kon）
题面
放学后茶会的几人决定去毕业旅行！但是她们关于该去哪里旅行有一点小分歧，所以她们决定用阿弥陀签来抽签决定目的地。话虽这么说，但是 Yui 希望操纵抽签结果， 所以她来找你帮忙了！
上面是一个简化版的阿弥陀签的示例。一个阿弥陀签由 条编号为 的竖线和若于条高度互不相同的横线构成，每条横线在某个高度上连接相邻的两条竖线。简单来说，使用阿弥陀签抽签的流程如下：
- 首先，选择一条竖线，将其最上端（高度最小的一端）作为起点；
- 然后，从起点开始向下走，每次碰到一条横线的一端，都必须走到其另一端再继续向下走。
- 这次抽签的结果就是到最下端时所在竖线的编号。
现在，Mio 正在制作一个阿弥陀签。目前签上已经画好了 条竖线，还没有任何横线，接下来她将在这个阿弥陀签上修改 次横线。每一次她会在某一个位置增加或者减少一条横线。Yui 在每次操作之后，想知道修改后的整个阿弥陀签至少删掉多少条横线，才能使得对于 ，以第 条竖线的最上端作为起点时，到达最下端时也在第 条竖线。你能帮帮她吗？
。
题解
可以将这个过程转化为有 个人分别从不同的起点开始走，每条横线视作将相邻的两个人交换，则我们的目标是使最终所有人回到原先的位置。
设每个人最后的位置为 ，则每次修改可以视为交换两个 ，最终的目标则转化为令 。
注意到对于所有 ，必定存在 个置换环，而每个置换环都需要 次删除操作（即删除其中一次置换对应的横线）来满足最终条件，因此最终的删除边数量就是 。
所以我们只需要开一棵线段树维护置换环数量即可。
T3-Q（tamako）
题面
在一个 的方格纸上的某些格子有障碍，使得剩下的所有格子可以用 的多米诺骨牌不重叠地填满。
将要在方格纸上额外选两个格子放置障碍，使得不再能用骨牌填满所有空格。有多少种选择两个格子的方案。
如果方案数超过 ，你需要输出 而非方案数。
。
题解
假设空格数量为 ，对整个方格纸进行黑白间隔染色，那么会有 个黑空格和 个白空格。由于删除两个同色格子一定会导致方格纸无法再用多米诺骨牌填满，我们至少有 种方案，所以 时一定输出 。
考虑 的情况。我们可以把输入中的所有空格当成点建一张二分图，两个点之间连无向边当且仅当它们对应的空格在方格纸上相邻。显然这个图一定存在一个完美匹配，我们先把这个匹配找出来。然后我们考虑数有多少个点对满足删完之后仍然存在完美匹配。
对于一对异侧点 而言，假设它们在原图中分别匹配上了 ，删除这对点之后是否仍然存在完美匹配可以这样判断：我们先取消 在原图中的匹配，然后删掉这两个点，检查 是否是一条合法的增广路。具体来说就是，是否存在一条从 到 的路径 ，满足 都是原图中的匹配。我们枚举所有的 ，从 开始 bfs 所有可行的 即可。
记答案上限为 ，那么时间复杂度是 的。
T4-终（hotel）
题面
有一个由 A 和 S 构成的字符串。
这群史莱姆会进行以下四种操作：
A进行分裂：在一个A的两端各增加一个S。即将字符串中的某个A替换为SAS。S进行分裂：在一个S的两端各增加一个A。即将字符串中的某个S替换为ASA。A组团逃跑：连续 个A可以消失。即删除字符串中的连续 个A。S组团逃跑：连续 个S可以消失。即删除字符串中的连续 个S。
给出两个常数 和 ，有两个字符串 和 ，求是否能将 经过若干次操作转换为 。
。
题解
记 表示空串， 表示字符串 重复 次。
经过足够的手玩，我们可以发现：
，同理 。
，同理 。
，同理 。
，同理 。
，同理 。
所以，我们可以在一个非空串的任何位置添加 和 。也就是说：
，同理，。
，同理 。
就是说，所有操作都是可逆的，那么：
。 显然答案只与 和 有关，所以下面只考虑 且 的情况。不妨设 。
对于任意的 ， 和字符串 ，我们考虑以下对字符串 的操作：
- 首先，假如 R 中存在子串 SA，将其替换为 ASSS，直到所有 S 都在 A 右侧为 止。
- 随后，消去所有连续的 A4 和 S 4。
- 随后，如果有至少两个 S，将最前面的 SS 替换为 AA。如果有 A4 就消去。
显然，经过这样的操作后，R 一定是以下八个串之一：
。我们将这些串称作标准串。
当然， 之后并不能进 行任何操作，你可以把它当成 ，这并不重要。
那么，我们只需要考虑分类讨论一下，在不同的 和 下，这八个串之间哪些能互相转移即可。
对于 的情况，这八个串之间并不能互相转移。证明也很简单：显然最后得到的串只跟上述第二步操作结束之后的字符串中， 和 的个数 的值有关。 题目中的操作 不会改变这两者的值，而操作 会使得这两者同时 。无论如何都不会改变最终的结果。
是平凡的。
时，相当于所有的 都不存在，那么 也不存在。此时只有 和 两种情况。
时， 和 仍然不存在。有 四种情况。由于 时 的数量的奇偶性不会改变，所以这些情况下所有情况之间不能转移是显然的。
所以，我们只需要求出 和 对应的标准串，并看它们能否互相转移即可。
时间复杂度 。
题解：P9352 [JOI 2023 Final] 训猫 / Cat Exercise
· 阅读需 5 分钟
题目链接
题意简述
一棵树上有 个权值不同的点，一开始有一只猫位于树上权值最大的点上。
每次可以选择在一个点上放置障碍，如果猫所在的点被放置障碍，则它会沿简单路径移动到能到达的点中权值最大的一个点上。
求能达成的猫的最大移动距离和。
解题思路
给出一个不太一样的思路。
考虑到因为给出的是一棵树，因此一旦离开某个点，就不可能到达与该点相连的其他点。
基于这一性质，实际上每次移动都会将猫的移动范围限制在上一个点的某棵子树内。
考虑进行搜索，传递状态为 ，搜索以 为根的子树内，从该子树内权值最大的点开始能达到的最长移动距离和。
对于权值最大点的子树，这是好做的，我们只需要将结果取最大值即可。
设 表示以点 为根的子树内权值最大的点，于是我们就要考虑如何处理在以 为根的子树内而在以 为根的子树外的点。
直接做显然不好做，但是因为以 为根的子树的内容不会影响到别的子树的结果。
所以我们可以在计算完以 为根的子树之后直接将这一子树删去，然后再对剩余部分直接计算贡献，可以发现实际上就是在计算在以 为根的子树内而在以 为根的子树外的点的贡献。
只需要用线段树维护 dfn 进行删点（将权值更改为 ）和查询区间最大值操作即可。
复杂度为
参考代码
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const ll N = 200005;
ll n , h[N] , fa[N] , dfn[N] , pos[N] , dfncnt = 0;
ll top[N] , dep[N] , siz[N] , son[N];
bool del[N];
vector <ll> g[N];
struct seg {ll l , r , mx , tag;} s[N << 2];
void dfs(ll u , ll f)
{
fa[u] = f; siz[u] = 1; dep[u] = dep[f] + 1;
pos[dfn[u] = ++dfncnt] = u;
for(auto v : g[u]) if(v != f)
dfs(v , u) , siz[u] += siz[v],
son[u] = (siz[son[u]] < siz[v] ? v : son[u]);
}
void dfs2(ll u)
{
if(!son[u]) return;
top[son[u]] = top[u];
dfs2(son[u]);
for(auto v : g[u]) if(v != fa[u] && v != son[u])
top[v] = v , dfs2(v);
}
ll lca(ll u , ll v)
{
while(top[u] != top[v])
{
if(dep[top[u]] < dep[top[v]]) swap(u , v);
u = fa[top[u]];
}
return dep[u] < dep[v] ? u : v;
}
ll dis(ll u , ll v) {return dep[u] + dep[v] - 2 * dep[lca(u , v)];}
void build(ll id , ll l , ll r)
{
s[id].l = l; s[id].r = r;
if(l == r) {s[id].mx = pos[l]; return;}
ll mid = (l + r) >> 1;
build(id << 1 , l , mid); build(id << 1 | 1 , mid + 1 , r);
s[id].mx = h[s[id << 1].mx] > h[s[id << 1 | 1].mx] ? s[id << 1].mx : s[id << 1 | 1].mx;
}
void pushdown(ll id)
{
if(s[id].tag)
{
s[id << 1].tag = 1; s[id << 1].mx = 0;
s[id << 1 | 1].tag = 1; s[id << 1 | 1].mx = 0;
s[id].tag = 0;
}
}
void update(ll id , ll l , ll r)
{
if(s[id].l > r || s[id].r < l || s[id].tag) return;
if(s[id].l >= l && s[id].r <= r) {s[id].tag = 1; s[id].mx = 0; return;}
pushdown(id);
update(id << 1 , l , r); update(id << 1 | 1 , l , r);
s[id].mx = h[s[id << 1].mx] > h[s[id << 1 | 1].mx] ? s[id << 1].mx : s[id << 1 | 1].mx;
}
ll query(ll id , ll l , ll r)
{
if(s[id].l > r || s[id].r < l || s[id].tag) return 0;
if(s[id].l >= l && s[id].r <= r) return s[id].mx;
ll la = query(id << 1 , l , r) , ra = query(id << 1 | 1 , l , r);
return h[la] > h[ra] ? la : ra;
}
ll find_ans(ll u)
{
ll v = query(1 , dfn[u] , dfn[u] + siz[u] - 1) , res = 0;
if(!v) return 0;
for(auto w : g[v])
if(w != fa[v] && !del[w])
{
ll tmp = dis(v , query(1 , dfn[w] , dfn[w] + siz[w] - 1));
res = max(res , find_ans(w) + tmp);
}
update(1 , dfn[v] , dfn[v] + siz[v] - 1); del[v] = 1;
if(u != v)
{
ll tmp = dis(query(1 , dfn[u] , dfn[u] + siz[u] - 1) , v);
res = max(res , find_ans(u) + tmp);
}
return res;
}
signed main()
{
freopen(".in" , "r" , stdin);
freopen(".out" , "w" , stdout);
cin >> n;
for(ll i = 1 ; i <= n ; i++) cin >> h[i];
for(ll i = 1 , u , v ; i < n ; i++)
cin >> u >> v , g[u].push_back(v) , g[v].push_back(u);
dfs(1 , 0); top[1] = 1; dfs2(1); build(1 , 1 , n);
cout << find_ans(1) << '\n';
return 0;
}
模拟赛题解/2025.8.26 模拟赛
· 阅读需 8 分钟
T1-运动会（sports）
题面
要将 个数分为两组，第 个数的值为 。
有 对关系 表示当第 个数和第 个数被分到同一组时，会产生额外 的贡献。
求分组之后两组之间总和差的最大值是多少。
。
保证对 ，有 且 。
题解
全相等，此时只需考虑朋友关系的贡献。
考虑如下贪心过程：设与 相关的朋友关系的默契度之和为 ，则选 从大到小排序后的前 个人分成一组，剩下的分成另一组，答案即为 。
证明：对于朋友关系 ，如果 (x,y) 在同一组，则对答案的贡献为 或 。否则，贡献为 ，即贡献被抵消掉了。\
复杂度 。
考虑每个人的力量，则将每个 额外加上 然后跑上述贪心即可。
T2-卡牌（card）
题面
有 张卡牌，每张卡牌背面有一个数字 ，正面空白。
初始全部正面朝上，可以做以下操作任意次：
- 选择一个 满足 。
- 翻转从左到右第 张牌的正反面，代价为 。
设最后背面朝上的卡牌写着的数的总和是 ，所有操作的代价总和为 ，则最终得分为 。
求最大可能得分。
。
题解
每个区间不交，对每个区间单独考虑，每个区间的贡献即为 。
显然每个 和每个 的区间都分别只会被操作其中一个。枚举翻转了 这个前缀，考虑每个 的区间。如果 ，则此时答案为 。
如果 ，则还需减去相交部分的和。分别维护即可。
考虑做如下转化：初始答案为 。若最后无法翻转 ，视作花费 的代价操作 这个点。
因此，初始时先将每个 加入操作中，即转化为操作若干次使所有卡片都被翻转的最小代价。\
我们考虑 建这样一张图：点集为 ，边为所有的 和 ，然后求 至 的最短路即可。易证一条 至 的路径对应了一种将所有卡片翻转的操作方案。
复杂度 。
T3-队形安排（formation）
题面
有 个同学，第 个同学的初始位置为 ，需要将每个同学的位置向左或向右移动 个单位。
需要将同学分为若干排，设一共站成 排，第 排的同学的编号集合为 ，则定义凌乱程度为：
为给定常数，求所有可能的队形的凌乱程度的最小值。
。
题解
当 时。我们先将题意转化为要求每个人不动或向右移动 。
为了方便计算，称第 位置被覆盖，为当前位置有人，或者存在两个位置为 的人，使得这两个人被分在同一组，且 。设 表示位置 最终是否被覆盖，则答案为 。
我们的限制形如，对于一个位置 的人，要求最后位置 和 中至少有一个被覆盖。
考虑状态压缩。设 表示考虑到位置 ，前 个位置的覆盖情况为 。设移动后最左和最右的人的位置之差为 ，则这样的状态总数是 的。由于 ，因此状态数可以接受。
考虑如何转移。设从左到右到了 ，枚举位置 是否被覆盖。如果存在一个人的初始位置为 ，则需要要求 被覆盖或者 被覆盖，这是容易判断的。贡献直接按照上述式子计算即可。复杂度 。
考虑 较大的情况。修改一下状态，设 表示位置 的覆盖情况为 从 转移到 。所需要的判断和贡献计算都是类似的。此外，我们需要额外记录下 的状态，以便在计算完后计算 和 之间产生的贡献。
这个算法的复杂度为 ，在 时可以接受。于是我们在 时运行上一个算法，在 时运行该算法，即可通过所有数据。
T4-二零四八（game）
题面
有一棵 n 个结点的树，初始 号结点上有一个数 。
一轮游戏的过程如下：
- 每次可以选择一条边，满足这条边两个端点上的数相等。然后，把这条边缩成一个新点，新点上的数为两个端点上的数之和。
- 如果在重复执行以上操作后，能使树上仅剩一个结点，那么你将获得游戏的胜利。
将进行 轮游戏。每轮游戏开始前，会交换某条边两个端点上写着的数。
对于每轮游戏，你想知道是否存在一种方案使你能获胜。注意，每轮游戏之间是独立的，但是修改是永久的。
。
题解
时，按值从小到大操作，发现合法的充要条件是，对于当前操作到的值 ，所有点值为 的点的导出子图有完美匹配。于是从小到大模拟收缩的过程。
带修改，我们需要一个更好的判定合法的方式，即需要快速对每个操作到的 ，判定其导出子图是否有完美匹配。
这里给出一个结论：假设一个有根树的某些点被染为黑色，其余点为白色。记黑点总数为 ，子树内有奇数个黑点的子树个数记为 。此时有 。
等号是否成立即为黑点导出子图是否有完美匹配的充要条件。
严格证明可以使用归纳法。感性理解：对于一个黑点 满足它的子树黑点数为奇数，那么 的父亲必须为黑点。所以这样的子树必须有 个。
于是我们可以把这个问题拆为两个子问题：对于所有 ，求操作到 时点值为 的点的个数，以及求此时有多少个子树内部点数为奇数个 。
对于第一个子问题，由于修改并未改变数值性质，所以可以在询问前预处理。
对于第二个子问题，我们考虑计算出每个子树的点值之和 ，那么这个子树在操作到 时做贡献。可以用 set 启发式合并维护二进制位，进位数量 的，可以直接维护。
对于修改，我们发现只会影响这条边深度较大的那个点的子树内，修改形如减去一个 再加一个 。我们把操作拆到在这个点上，在 set 里维护 的连续段，即可做到 加减一个二进制位。
总复杂度 。
模拟赛题解/2025.8.25 模拟赛
· 阅读需 8 分钟
T1-字符串排序（sort）
题面
给出 个仅包含大写字母的字符串 。
对于每次操作，可以选择任意一个字符串，将其内部的字符任意重排，记进行完重排后的字符串为 。
字符串 的字典序小于字符串 ，当且仅当存在一个正整数 ，满足 和 相同，且 ，或 和 相同且 。
求出是否存在一个方案使得对于任意 ，。
若存在，请求出一种方案。
。
题解
首先有一个很直接的贪心思路：从左到右考虑所有字符串，重排它使得它在字典序 前一个字符串的情况下，最小化其字典序（即留给后面的字符串更大的操作空间）。
考虑模拟这个思路，对于每个字符串尝试从左到右逐位确定某一个位置最小能填什么：从小到大枚举该位置上的字符，并检查在这一位填入该字符是否满足条件（即这个位后面的剩余字符从大到小填，能否使当前字符串字典序 前一个字符串）。
复杂度 。
T2-表白（love）
题面
有 个数 。
给出区间 ，要求在 中选择若干个数，满足其乘积对 取模的值最大。
对于每一个询问，求出得到的最大值。
。
题解
首先考虑
定义 表示 区间，能不能凑出 ，转移是平凡的。
考虑优化掉一个 ，dp 状态的结果只有 太浪费了，重新定义 表示最大的 满足只使用 的元素能凑出 。
特别的，当 都不能凑出 时 。
对于每一个询问，考虑枚举答案，即最大的满足 的 。
复杂度 。
T3-树上棋盘（tree）
题面
有一棵有 个节点的树，树上每个节点有一个权值 ，，保证每个权值都恰好出现 次。
定义得分为树上满足以下条件的节点二元组 的数量：
- 之间有边直接相连；
- 。
可以进行若干次交换操作，每次操作可以选择两个节点并交换它们的权值，每个点上的权值最多经历一次交换。
求能够达到的最大得分和对应的交换方案。
， 条边构成一棵树。
题解
使用贪心或者 DP 求解一个树上的最大匹配 ，则答案不会超过 。
大胆猜测答案一定可以取到 （到这里已经可以获得第一问的 分），以下是构造方法：
对于上面的最大匹配 ，构造一个有 个结点的无向图 ，连边 。
由于原树上每个结点在最大匹配中最多出现一次，而 在 中恰好出现两次，所以该图中结点度数不超过 。
我们先引入一个叫做“缩二度点”的操作：假设在 中，对于结点 有边 和 ，那么意味着在最大匹配中有两条边满足 和 ；
此时交换 ，即可以将匹配中的边调整为 和 。——对应到 中，相当于删除了边 和 （ 直接满足条件，可以不管了），加入了一条新边 ，十分类似广义串并联图中的“缩二度点”操作。
考察 的性质，由于结点度数不超过 ，所以 中的每个连通块要么是一个环，要么是一条链：
使用上面的“缩二度点”操作，一个环可以被缩成一个单点（即环上所有结点全部调整完毕），而一条链最后必然被缩成 的形态：思考造成这种现象的本质，由于这两个结点度数都为 ，那么满足 的某个 必然没有被选入最大匹配中。
此时只需要将 在匹配中对应的结点和那个没被选入的 交换即可。
根据不同实现，时间复杂度为 或 。
T4-橡子 5（acorn）
题面
有一棵有 个节点的树，节点编号为 ，给定常数 。
对于一个节点 ，定义 为：
- 以结点 为根，并据此将树的边定向使其成为一棵叶向树：具体地，若在以 为根的情况下， 为 的父亲，那么边 被定向为 。接下来可以添加 条从 出发的有向边，终点任意。令 表示 到 的最短路，答案为所有加边方案中 的最小值。
在某些测试点中，只需要对于 求出 ；而在另一些测试点中，需要对于 均求出 。
，输入数据保证形成一棵树。
题解
首先考虑如何判断一个答案是否可行。
设我们现在判断答案为 是否合法，我们可以从下往上做，每次将最深的点拿出来，此时的操作应该是其 级祖先向根节点连边，这样这一整颗子树都是合法的，删掉这个子树。
重复上述过程 次后判最深的点是否和根的距离小于等于 ，即为 是否合法。
将这棵树拍到 DFS 序上，用线段树维护最深的点，删子树可以变成一个区间减 。这一部分的时间复杂度为 。
考虑换根怎么做。首先线段树上维护的是每个点到深度的距离，设当前的根为 ，换根后为 ，只需要将 子树内到根的距离减一， 子树外到根的距离加一，这个也是容易维护的。 接下来就剩下树上 级祖先和换根后的子树，这个比较经典，分讨就可以了。
具体的，以 为根， 的树上 级祖先可以如下分讨（记 和 在原树上的 lca 为 ）：
- 若 ，则 的树上 级祖先为原树上的 级祖先；
- 否则，则 的树上 级祖先为原树上 的 级祖先。
以 为根， 的子树为：
- ，此时 的子树为所有点；
- 原树中， 在 的子树内，设 为 路径上倒数第二个点，此时 的子树为除原树中 的子树以外的所有点；
- 否则， 的子树不变。
对于每个点都二分一下可以做到 ，精细实现可以通过。
但是还可以做到更优。发现换根后答案的变动不会超过 ，可以将 次判断缩到 次。
此时时间复杂度为 。
模拟赛题解/2025.8.24 模拟赛
· 阅读需 7 分钟
T1-字符串(string)
题面
给定一个长为 的仅由小写字母组成的字符串 。
可以选择两个正整数 满足 ，对 的区间进行翻转。
求通过一次翻转，最多能得到多少种不同的字符串。
。
题解
注意到，对于所有首尾字符相同的子串，它的反转操作都能等效为去掉其首尾字符的新子串的反转操作。
所以我们只需要统计有多少个点对互不相同即可。
T2-子序列(subsequence)
题面
给定一个长度为 的整数序列 ，对其每个子序列求和可以得到 个数，求其中前 小的数。
。
题解
如果 非负，可以观察到我们每次增加只会是增加一个数或者替换一个数，我们用一个优先队列存储，可以 解决。
考虑有负数的情况， 设负数是 ，我们直接将 换为 ，选/不选的情况就会从 变成 ，注意到我们只需要将所有答案减少 ，此时的情况就与原本一致，按照全是正数计算即可。
T3-划分(divide)
题面
有一个 的网格，第 行第 列的格子记作 。
定义一个级别 的 型为两边长（包括拐点）均为 的 型，可以旋转，特殊地，级别 的 型仅包含一个方格。
给定格子 ，考虑将整个网格划分为级别 的 型各一个的所有方法（划分时每个格子属于且仅属于一个 型），求 属于的 型的级别之和，结果对 取模后输出。
。
题解
最简单的写法是计算有多少种方法能使 被分在 级别的 型里，设为 。
从大往小看，可以认为每次操作会使矩形上下缩一行，左右缩一列（或者可以认为矩形左上角最多往下移一行，最多往右移一列，矩形大小减 ）。
如果要把这个格子分到 级别的矩形里，那么前 次缩矩形就不能把这个点缩没，分行列考虑，删掉最上方行的次数必须在 范围内，同理删掉最左边列的次数必须在 范围内，后边操作就是任意的了。
因此方案数就是 。
时，两个括号内都是 ，式子结果是 。
随着 的减小 增大，且 的项数会少，这可以利用杨辉三角观察一下这一段和的规律，先乘 推到下一行的一段区间 （会带点零碎的边界），再简单加减几项调整一下（减掉多余的贡献，如果缺项就加上缺少的项），这样可以做到 递推。
本题中应该是乘 后原来那行最左最右的两项的贡献会算多一倍，所以应该就是减原来那行首尾两项，不用加。
最后答案可以用 （也就是 ）减去前边每一项，相当于初始认为每一种方案级别都是 ，然后减去级别 的方案（这些方案的级别都损失了 ），然后减去级别 的方案（这些方案的级别又损失了 ），以此类推。
也可以用 算出级别恰好为 的方案数。
甚至可以直接分这个点出现在级别恰好为 的 型的角还是边上直接列出组合数前缀和形式的式子计算，但写法不如计算 的简便。
时间复杂度 。
T4-逆序对期望(reverse)
题面
现在你有一个 个数的排列 ，你可以对它做两种操作：
- 交换两个相邻元素；
- 将整个排列随机打乱，随机打乱后出现任意一种排列的概率都是相等的 (即都是 )。
现在你最多对这个排列执行 次操作（可以少于 次）。整个过程中，你可以根据当前的排列情况，实时决策下一步是否停止操作，以及使用 1/2 哪种操作。
请问最优策略下，最终排列的逆序对数期望的最小可能值。
题解
记 为输入排列 中逆序对数量。
只有第 种操作时，由于交换相邻元素只能让逆序对数 ，答案为 。
只有第 种操作时，随机打乱后的逆序对数期望是一个定值，可以通过 DP 求出。设计 代表 这些数随机打乱之后恰好有 个逆序对的概率，转移为 。
利用前缀和优化可以在 时间完成。
令 代表长度为 的随机排列，进行 次打乱之后的逆序对期望。
那么每次打乱之后都可以进行决策，停下来或者继续打乱（期望为 ），设当前逆序对数为 ，若 则停下来，否则继续打乱。
设
答案为 。
两种操作都有时，需要进行决策是否先使用操作 进行打乱，令 代表长度为 的随机排列，进行 次最优操作之后的逆序对期 望，设当前逆序对数为 ，转移有2种：
- 使用 次 操作，得到的逆序对数量为 先打乱，得到的逆序对数量为
- 先打乱，得到的逆序对数为
两种择优转移：若 使用第1种转移，否则第2种转移。设 。
维护 和 的前缀和 s1_{i,j}$$s2_{i,j}，上式可以写成
可以在 时间内预处理出 数组，答案为 ，总复杂度 。
注意空间较大，可以将 数组滚动。
模拟赛题解/2025.8.23 模拟赛
· 阅读需 8 分钟
T1-亲爱的（habibi）
题面
统计一个字符串 中共有多少个子序列，满足：
- 长度为 。
- 前 个字符两两不同。
- 第 个字符与第 个字符相同。
- 第 个字符与第 个字符相同。
答案对 取模。
， 中仅包含大小写英文字母和数字。
题解
考虑设计 dp。
设计状态 表示从位置 开始且必定选择 ，形成形如 的长为 的后缀的方案数。
首先 必有一个为 ，可以使用滚动数组降一维，记录当前左边每个数剩余的数量，容斥可以得出左半部分的方案数。
复杂度为 。
T2-收藏（collect）
题面
有一个长度为 的序列，每次可以从最左端和最右端取出一个数，并放在当前已取出的数列的末尾。
共有 个序列，要求对每个序列求出最后得到的数列的最长可能 LIS。
。
题解
可以发现操作过程本质上是将序列划分成两段，将后缀翻转后归并两个序列。
在划分序列后，LIS 的上界已然确定，是所有得到的序列的 LIS 长度之和，因为若总 LIS 长度更大，其位于这 个子序列中的部分必然有一个的长度超过该子序列 LIS， 矛盾。
达到这个上界是简单的，只需将求得的子序列 LIS 归并起来。进一步，发现序列的贡献是独立的，只用对每个序列都找到最优划分。
暴力枚举划分并计算左右两段 LIS 显然无法通过。发现瓶颈在于反复计算前后缀 LIS，考虑先通过扫描线+BIT 和指针的方式先处理出每个前后缀的 LIS 长度及 LIS 中离当前位置最近的数，再枚举划分并求得最优位置，找出前后缀 LIS。序列之间的归是简单的。
复杂度为 。
T3-棋盘（chess）
题面
有一个 的棋盘，双方轮流放黑白子。
每有一行或一列不完全相同，玩家得一分，每有一行或一列完全相同，对手得一分。
最终若玩家分数为奇数且对手分数为偶数则玩家胜利，否则对手胜利。
求最终能让玩家获胜的棋盘状态得方案数。
。
题解
可以发现你获得的分数和 AI 获得的分数相加等于 。则 为偶数时，一定不存在合法解。又因为当 为奇数时，若你获得的分数是偶数，那么 AI 一定是奇数，反之亦然。故两者一一对应，只需要求出其中一种方案数即可。
一整行或一整列颜色不完全相同的情况难以处理，所以考虑处理一整行或一整列颜色完全相同的情况。即现在需要解决这个问题：一整行或一整列颜色完全相同的数量是偶数的方案数。再反过来，先考虑为奇数的方案，再用总方案去减。
根据惯用做法，直接容斥/二项式反演。先考虑容斥系数的求解：对于答案至少有 个产生贡献的情况，恰好 是最后一次计算。
- 当答案至少有 个产生贡献时：容斥系数为 。
- 当答案至少有 个产生贡献时：之前产生 的贡献，所以此时容斥系数为 。
- 当答案至少有 个产生贡献时：之前产生 的贡献，所以此时容斥系数为 。
- 当答案至少有 3 个产生贡献时：之前产生 的贡献，所以此时容斥系数为 。
- 当答案至少有 3 个产生贡献时：之前产生 的贡献，所以此时容斥系数为 。
所以答案至少为 时，容斥系数为 。
考虑如何计算答案：
- 只有行产生贡献时，答案是 。具体含义为从 行中选择 列颜色相同，他们颜色方案数为 。其余位置方案数为 。
- 只有列产生贡献时，答案是 ，与行同理。
- 都产生贡献时，答案是 ，考虑枚举行与列分别的贡献，如果列的颜色相同，行的颜色也相同，那么总的颜色只有全黑和全白两种。
对第三个式子进行优化：
因此转移的复杂度就可以做到 。
T4-吃饭（eat）
题面
共有 个数，每个数为 。
有一个序列 ，要求前 个数的中位数是 。
可以任意调整 的顺序，但是不确定序列 ，求有多少种序列 可以被满足。
答案对 取模。
题解
先尝试找出满足 的充要条件。简化问题，先考虑 构成 到 的排列的情况。
容易知道 ，因为至少有 个数比 小或大。同时，序列中位数从 变化为 的过程中，由于只加入 和 ，所以中位数至多挪动一位。则 到 的取值不能在 与 之间。于是可推出 到 的取值不在 与 之间。
可以证明满足这两条限制是充分的。只需要构造出合法 序列。若 ，则加入目前不在序列中的最小和最大的 。若 ，则若 还不在序列中则加入 和目前不在序列中的最大数，否则加入两个最大数。 同理。容易验证这样的构造是合法的。
接下来考虑如何 dp 求解。倒过来考虑，这时第一条限制可认为是每次解锁 和 两个取值，第二条限制可认为是 到 之间的所有取值都要被删去。设 为已确定 及之后的取值，此时还未被删去的取值中还有 个比 小， 个比 大，这样的方案数。（没有必要记录具体取值，只需要记录相对位置）转移只需要考虑 的取值，并删去 与 的之间取值，并解锁最小最大两个新取值即可。
最后解决 重复的问题。这需要将每个 的取值改变为在 序列中的排名。那就希望相同的 对应的排名尽量相同（少被第二条限制删掉），且尽量早地摆脱第一条限制。所以只需要判断相同取值的 排名中哪一个最早摆脱第一条限制，并将所有 都设为这个排名即可。于是 dp 时只需要判断新解锁的取值是否和前面重复，来决定是否对 或 加一。
时间复杂度 。
模拟赛题解/2025.8.22 模拟赛
· 阅读需 5 分钟
T1-那头与分配（distribute）
题面
有一棵有 个节点的树，树上每个节点有权值 ，每次操作可以将一个点上的权值部分转移到相邻点。
问最后是否能使每个结点的权值相等。
。
题解
注意到一条边不会产生贡献当且仅当其两侧的头的个数平均值相等。
对于产生贡献的边，也可以计算出这条边会转移的权值的数量。
考虑得到一个合法顺序：随便选一个点为根，然后先把从深往浅把大于平均值的子树往根转移，再从浅往深向小于平均值的子树转移。
容易发现这样做任意时刻转移的 ， 故方案合法。
T2-那头与锻炼（train）
题面
一棵树上有 个权值不同的点，一开始有一个那头位于树上权值最大的点上。
每次可以选择在一个点上放置障碍，如果那头所在的点被放置障碍，则它会沿简单路径移动到能到达的点中权值最大的一个点上。
求能达成的那头的最大移动距离和。
题解
分析：考虑到因为给出的是一棵树，因此一旦离开某个点，就不可能到达与该点相连的其他点。
基于这一性质，实际上每次移动都会将猫的移动范围限制在上一个点的某棵子树内。
-
官 sol
考虑时间倒流，用并查集将几个子树合并成一个，维护其贡献，树上 dp，复杂度
-
特殊做法
本质上就是搜索，传递状态为 ，搜索以 为根的子树内，从该子树内权值最大的点开始能达到的最长移动距离和。
在计算完以 为根的子树之后直接将这一子树删去，然后再对剩余部分直接计算贡献，可以发现实际上就是在计算在以 为根的子树内而在以 为根的子树外的点的贡献。
用线段树维护 dfn 进行删点（将权值更改为 ）和查询区间最大值操作即可。
T3-那头与串串（string）
题面
对于一个字符串，若其可以由多于一个相同的字符串相连构成，则称其为好的字符串。
求对于一个字符串 ，最少需要删除几个点才能使该字符串变成好的字符串。
，保证 由小写字母构成。
题解
设最后被分为 段，考虑到对 进行分开处理。
当 较小时，直接枚举最终得到的字符串的分界点，对所有被分开的字符串求 LCS，可以使用 dp 解决，复杂度 。
当 较大时，因为单个循环节的长度不会太大，所以考虑枚举 ，即单个循环节，贪心地在 中匹配 ，复杂度为 。
对于 使用第一种，对于 使用第二种，复杂度即为 ，跑得飞快。
T4-那头与陷阱（trap）
题面
在一个数轴上有 个陷阱，每个陷阱占据了 的所有位置。
有两种行动方式：
第一种是向右一个单位，花费 的时间。
第二种是向右 个单位，花费 的时间。
每次移动都需要移动到的位置不能被陷阱占据， 给定。
共有 个计划，第 个计划是从初始位置 移动到位置 ，求对于每个计划，完成计划的最短时间，如果不能完成计划，输出 。
题解
根据 和 的大小关系分类讨论。
较为简单的情况是 ：此时需要最小化跳跃次数。设 表示到达 需要最少跳跃几次。转移是简单的 。尝试分析 的结构。对于一段可以到达 的区间，无法到达的位置构成一个前缀。
实际上，剩余部分的 fi 值是相等的，也就是在一 段内不存在一个位置 使得 。可以归纳证明，假设前 段每段相等且总体递增，那么第 段也满足上述条件。快速维护是简单的。
对于 ，。每段无法到达的部分依然是一个前缀。有以下结论：有值的部分形如先一段值为 ，长度 的段，而后是长度为 的值为 的段。这个结论可以类似的归纳证明。所以只需要对于每段求出有值的第一个位置和值与第一个位置不同的第一个位置就可以表示整个 dp 数组。可以用二分套二分维护做到 ，也可以精细实现做到 。
询问只需要二分找到询问的位置位于那一段内然后就可以快速求值了。
模拟赛题解/2025.8.21 模拟赛
· 阅读需 5 分钟
T1-钢（hoi）
题面
一棵树上有 个点，每个点上初始权值为 。
两人先后选择一个点清除，并使其他所有点上的权值向这个点迁移一次。
当最后一个点被清除后，清除掉最后一个点的人获胜。
问在都选择最优策略的情况下，谁能获胜。
题解
可以将清除这一过程转化为树上所有除了所选的点之外的叶子节点被删除。
考虑树上的一条条链，每次变化会使树上的链长度减少 或 ，显然直径会最后被删完。
因此只需要考虑直径，将每次操作转化为使链长减少 或 ，这就是一道经典的小学奥数题。
T2-蒸（sgs）
题面
有一条长为 ，由 三种字符构成的字符串。
每次操作可以删除任意一个形如 之一的子序列。
如果能删除整个序列，就可以获得 的值， 给出， 分别代表字符串中 的数量。
给出 ，求对于所有数量为 的起始字符串长度，可以得到的值的和。
题解
对于这样的字符串删除，考虑将其转换为字符串匹配（什么神仙思路）。
观察到对于所有可删除的子序列， 都在末尾，将其转化为右括号。
因为存在 ，所以我们将 转化为一个左括号，将 转化为两个右括号。
又因为存在 ，所以考虑将 转化为两个左括号或者一个右括号，代入 发现没问题。
又因为若存在两个 将前一个当作左括号，后一个当作右括号一定是没问题的。
于是设 表示当前填充到第 位，剩余 个左括号， 目前是否出现过被当成右括号的 的情况下的最大权值和，转移是不难的。
T3-原（gen）
题面
有一个长度为 的序列 ，可以进行若干次操作，每次操作形如 ，可以将 的所有数改为 或 ，若 为 则将区间改为 ，若为 则改为 。
如果能将序列更改为给定的序列 则视为获胜，求出是否能获胜，如果能，给出操作方案，要求操作次数不超过 。
题解
首先，根据操作的性质，我们注意到不可能将形如 的序列转换为 ，即不能改变数字间的顺序。
因此我们只需要能在 序列中找到一个顺序包含 序列中所有数的子序列则有解。
考虑如何构造方案，可以将 中的子序列和 中对应区间分类考虑，设 中位置为 ， 中对应区间为 。
- ，此时将 一次覆盖完之后必须要让其他数字覆盖 的区间。
- ，此时将 一次覆盖完之后必须要让其他数字覆盖 的区间。
- ，此时只需要用一次（ 或 ）或两次（）将 覆盖完即可。
并且，因为 和 是单调递增的，因此构成一定是一段前缀属于情况 ，一段后缀属于情况 ，其余部分属于情况 。
因此我们构造情况 为按 递减顺序做，情况 为按 递增顺序做，情况 可以随便做。
证明操作次数：我们考虑到，对于 需要做两次的情况当且仅当 ，但此时实际上覆盖了长度至少为 的区间，而其他情况下都只需要做一次操作， 不会出现重复，所以总的操作次数一定不超过 。
T4-诡（lom）
题面
有一个长度为 的序列 ，要将其划分为若干（）个区间，每个划分方案的贡献是所有区间的极差之和。
每次操作将选择一段区间并将该区间内所有数增加 ，并求出每次修改后的最大划分贡献，询问不独立。
题解
考虑原序列的差分序列，显然可以发现当取到最大值时需要使一段区间内全部同正或同负。
那么只需要考虑每段差分序列的左右两边是否被选既可。
每次操作相当于两次单点修改，使用小清新线段树即可通过。
模拟赛题解/2025.8.20 模拟赛
· 阅读需 6 分钟
T1-天元超常 2（super）
题面
给出一个 个点， 条边的无向图，每条边有初始颜色 和目标颜色 。
每次操作可以选择一个点将其所有连边转换成任意相同颜色。
需要给出一种操作方案使得图上所有边都变为其目标颜色 ，或者报告无解。
，其中 表示颜色个数。
题解
首先我们注意到，每次操作的处理都要考虑后续带来的变化，而不需要考虑之前的操作。
所以我们倒序地进行操作的分析。
此时问题就被简化成需要找到每一个周围所有 都相等的点。
于是这就是一个类似于拓扑排序的问题，每次处理的时候使得一部分边不用考虑，再把新产生的符合所有 都相等的点加入。
最后当没有点可加入时，假如剩余的所有边都是 的，就可以输出答案，反之则无解。
用队列维护点，map 或诸如此类的东西维护边的类型，复杂度
T2-团计数（counting）
题面
对于一个 个点， 条边的简单无向图，求这张图中团的个数对 取模。
对于一张图 ，其点集的一个子集 被称为一个团当且仅当其导出子图是完全图。
题解
首先这题是一个 #pc 问题，不存在多项式复杂度的解法，因此我们考虑指数级的算法。
因为边数不超过 ，而一个团内的边数是阶乘级别的，所以显然一个团内的边数不会太多，因此考虑让指数上为 级别。
我们考虑如何缩减每个点的度数，可以使用类似三元环计数的处理方法，将所有点按照编号从小到大排序，只保留编号较小的点到编号较大的点的连边，则新图上每个点的度数是 级别的，计算答案时枚举每个团中度数最小的点即可。
而 仍有 ，显然无法接受，但是可以考虑折半搜索，枚举前后各 个点，复杂度就会被控制在合理的范围内。
最后使用 SOSDP 即可，该算法可以在 的时间复杂度范围内计算出度数为 的点对答案的贡献，因此总复杂度约为 ，常数相当小，可轻松通过。
T3-原野（field）
题面
有一个 大小的矩形，其上每个位置都有一个值。
求有多少个子矩形，满足该子矩形内所有值都严格小于与这一位置横坐标或纵坐标相同的边界上的值。
题解
我们注意到因为要求矩形内的数严格小于对应边界上的数，对于 的情形，合格的 构成嵌套集，即不会出现两组 和 满足它们对应的线段既不是相离关系也不是包含关系， 同理。
因此，对于每一个 ，可能成为答案的 只有 组， 同理。求出这些区间可以使用单调栈，这部分是 的。
考虑一个矩形合法的充要条件，假设 和 合法，我们相当于要让 合法（A），以及 合法（B）。
我们可以对于每个合法的 ，预处理出 表示 时 性质才满足， 性质同理，时间复杂度同样为 。
枚举矩形的左上角，相当于要求满足条件的 二元组使得 。这是一个二位数点的形式，可以使用树状数组求解，复杂度 。
T4-旅途（journey）
题面
在一个 个点的数轴上，第 个点可以一步到达 中的点，保证 。
可以选择一个点出发，经过一段时间后再次回到这个点，每个点可以走超过一次，设这段路程经过点的点集为 。
求有多少种不同的 是可能达到的。
题解
考虑如何 check 一个 是否合法。首先题目中的要求等价于 对应的导出子图强连通。
结论是，我们每次将 中相邻的两个互相可达的 SCC 合并（初始时，每个点自成 一个 SCC）， 合法当且仅当通过上述过程可以将 合并为一个 SCC。
证明大概就是考虑假设某次合并了不相邻的两个 SCC，那么一定也可以调整为若干次合并相邻的两个。
但是直接这样做会算重。一种处理方法是，补集转化， 不合法当且仅当最后留下 了 个 SCC 且相邻无法合并。
记 表示 ，， 的合法 的数量，同时维护一个辅助数组表示若干个相邻之间无法合并 的 SCC 拼起来的方案数即可。时间复杂度视实现在 之间，由于常数很小理论上均可通过。
题解：CF2043D Problem about GCD
· 阅读需 3 分钟
题目链接
题意简述
给出三个整数 ，要求找到一个数对 满足 且 ，并且满足 最大。
如果有多组解，选择 的值最小的一个。
解题思路
首先 肯定都是 的倍数，所以直接将 转化为 ，在该区间内求最远互质点对，设为 ，则 。
关于如何求区间内最远互质点对，可以参考 Atcoder arc137_a（站内链接）。
如果直接暴力枚举 和 ，理论复杂度达到了惊人的 ，看上去是不能通过的。
但是其实并不会遍历那么多次，参考上面给出的题解可知在题目给出的 数据范围内复杂度并没有很高。
所以尽管并未算出实际复杂度期望，但是我们暴力枚举仍然可以通过本题。
参考代码
#include <bits/stdc++.h>
using namespace std;
long long T , l , r , g;
long long gcd(long long aa , long long bb) {return bb ? gcd(bb , aa % bb) : aa;}
void solve()
{
long long len = r - l;
while(len >= 0)
{
for(long long i = l ; i <= r - len ; i++) if(gcd(i , i + len) == 1) {cout << i * g << " " << (i + len) * g << '\n'; return;}
len--;
}
cout << -1 << " " << -1 << '\n';
}
int main()
{
cin.tie(nullptr)->sync_with_stdio(false);
cin >> T;
while(T--)
{
cin >> l >> r >> g;
l += g - 1; l /= g; r /= g;
solve();
}
return 0;
}
补充
以下是不严谨的关于该代码时间复杂度的证明。
参考资料
证明
在维基百科的这一条目中提到，托马斯·雷·奈斯利使用了公式 来计算素数间隙与克拉梅尔猜想相契合的程度，对于现在已知最大的素数间隙， 的值依然保持在 左右。
因此该题目中最大的素数间隙（设其为 ，且 表示最大的质数间隙对应的质数对中较小的那一个）在 左右，因此即使我们并不确定 的具体值， 的值一定不会超过 ，而该式的值约为 。
在该题目中，能够构造出的最坏情况为 分别距离 为 ，此时上述代码的时间复杂度为 。
又因为我们已经证明了 的值并不会超过 ，所以上述代码的最坏时间复杂度为 ，不超过 ，显然可以通过本题。
题解：P11293 [NOISG2022 Qualification] L-Board
· 阅读需 2 分钟
题目链接
解题思路
考虑维护四个数组 分别表示以位置 为起点，在其上、下、左、右四个方向上，一定选择该点的最大区间和，显然可以 DP 维护。
时间复杂度为
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1005;
int n , m;
long long a[N][N] , u[N][N] , d[N][N] , l[N][N] , r[N][N];
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for(int i = 1 ; i <= n ; i++)
for(int j = 1 ; j <= m ; j++)
{
cin >> a[i][j];
u[i][j] = max(u[i - 1][j] , 0ll) + a[i][j];
l[i][j] = max(l[i][j - 1] , 0ll) + a[i][j];
}
for(int i = n ; i >= 1 ; i--)
for(int j = m ; j >= 1 ; j--)
{
d[i][j] = max(d[i + 1][j] , 0ll) + a[i][j];
r[i][j] = max(r[i][j + 1] , 0ll) + a[i][j];
}
long long ans = -0x3f3f3f3f;
for(int i = 1 ; i <= n ; i++)
for(int j = 1 ; j <= m ; j++)
{
ans = max(ans , max(l[i][j] , r[i][j]) + max(u[i][j] , d[i][j]) - a[i][j]);
}
cout << ans << '\n';
return 0;
}
题解：P9827 [ICPC2020 Shanghai R] Sky Garden
· 阅读需 13 分钟
题目链接
解题思路
本题的 做法已有，不多说。
@lailai0916 在他的题解中给出了使用数学工具进行归纳的 做法，十分优雅，下面来看看人工队的表现。
设点 在第 个圆上，点 在第 个圆上，二者之间相隔 条直线（包括点 所在的直线，不包括点 所在的直线）， 为 。
因此
所以此时题目要求的就是：
我们注意到， 必定小于等于 ，并且两点之间的最短路一定是经过圆心或者只经过一条线段再经过一条圆弧（仅取决于两个点所在直线的角度大小）的，于是我们就得到：
- 然后开始化简：
- 分别化简：
- 合并回原式：
- 化简 ：
化简 ：
化简 ：
-
化简 ：
-
化简 ：
-
化简 ：
-
全部代入回原式：
-
最后得出结论：
参考代码
#include <bits/stdc++.h>
using namespace std;
long long n , m;
inline long long tw(long long x) return x * x;
inline long long th(long long x) return x * x * x;
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
long long p = 2 * m / acos(-1) + 1 , p , q;
q = ((4 * m * th(n) - 8 * p * m * th(n) - 4 * p * m * n + 8 * m * n + 12 * tw(m) * th(n) + 12 * m * tw(n) + 12 * tw(m) * tw(n) - 12 * p * m * tw(n)) / 6 - ((m * n) * (n + 1)) * (m == 1));
p = ((3 * tw(n) * tw(p) - 3 * tw(n) * p + n * tw(p) - n * p + 2 * tw(p) * th(n) - 2 * p * th(n)) / 6);
cout << fixed << setprecision(12) << p * acos(-1) + q << '\n';
return 0;
}
题解：P3618 误会
· 阅读需 2 分钟
题目链接
参考资料
题意简述
给定 组数据，每组数据包含两个字符串 。可以将字符串 中与字符串 相同的字串删去，问最终有多少种字符串 可能的结果？
解题思路
看到字符串匹配首先想到 KMP 算法。
因为某一个字符串是否替换只影响与之相交的字符串（无后效性），所以考虑 DP。
设 表示前 位的替换方案数， 为当前已匹配到的 字符串位数，则：
于是就有了一个朴素的 KMP 混合 DP 的算法，时间复杂度为 ，甚至拿到了最优解 rk3。
参考代码（附注释）
#include <bits/stdc++.h>
using namespace std;
const long long N = 100005 , mod = 1e9+7;
long long T , n , m , p , nxt[N] , f[N];
string a , b;
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> T;
f[0] = 1;//最开始只有一种方案
for(long long k = 1 ; k <= T ; k++)
{
cin >> a >> b;
n = a.size();
a = '#' + a;
m = b.size();
b = '#' + b;
p = 0;
for(long long i = 2 ; i <= m ; i++)//预处理
{
while(b[i] != b[p + 1] && p)
{
p = nxt[p];
}
if(b[i] == b[p + 1])
{
p++;
}
nxt[i] = p;
}
p = 0;
for(long long i = 1 ; i <= n ; i++)//kmp加dp
{
while(b[p + 1] != a[i] && p)
{
p = nxt[p];
}
if(b[p + 1] == a[i])
{
p++;
}
f[i] = f[i - 1];
if(p == m)
{
f[i] = (f[i] + f[i - m]) % mod;//dp转移
}
}
cout << "Case #" << k << ": " << f[n] << endl;//别忘记输出格式
}
//system("pause");
return 0;
}
题解：P10773 [NOISG2021 qualification] Truck
· 阅读需 5 分钟
题目链接
解题思路
首先，我们注意到可以把运输的过程反过来，从 点开始，运送的价值初始值为 ，每走过一条边就产生一次代价，并将运送的价值加上这条边的 。
于是我们得到如下结论：
若有三个点 满足 在从 到 的简单路径上，
令 为从点 到点 的代价， 为从点 到点 的边权 之和， 为从点 到点 的边权 之和。
则有：
于是我们就可以用树链剖分加线段树维护答案。
参考代码（内附注释）
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 200005 , mod = 1000000007;
int n , G , Q;
int son[N] , dep[N] , siz[N] , fa[N] , top[N] , dfn[N] , pos[N] , tot;//树剖要用的数组
int beft[N] , befd[N];//化边为点
struct edge
{
int to , D , T;//存边
};
vector <edge> g[N];
struct seg
{
int sumd , sumt , up , down;//sumd和sumt含义如上，up表示在这个区间内从下往上走的代价，down表示在这个区间内从上往下走的代价
};
seg s[N << 1] , null;//null表示一个空点
seg operator +(seg x , seg y)
{
seg res;
res.down = (x.down + y.down + (x.sumt * y.sumd) % mod) % mod;
res.up = (x.up + y.up + (x.sumd * y.sumt) % mod) % mod;
res.sumd = (x.sumd + y.sumd) % mod;
res.sumt = (x.sumt + y.sumt) % mod;
return res;
}//将区间合并重载为加法
void dfs1(int u , int pre)//建树+预处理
{
fa[u] = pre;
if(u == 1)
{
fa[u] = u;
}
siz[u] = 1;
dep[u] = dep[pre] + 1;
for(auto [v , d , t] : g[u])
{
if(v == pre)
{
continue;
}
befd[v] = d;
beft[v] = t;
dfs1(v , u);
siz[u] += siz[v];
if(siz[v] > siz[son[u]])
{
son[u] = v;
}
}
}
void dfs2(int u , int pre)//树剖
{
dfn[u] = ++tot;
pos[tot] = u;
if(!son[u])
{
return;
}
top[son[u]] = top[u];
dfs2(son[u] , u);
for(auto [v , d , t] : g[u])
{
if(v == pre || v == son[u])
{
continue;
}
top[v] = v;
dfs2(v , u);
}
}
void build(int num , int l , int r)//建线段树
{
if(l == r)
{
s[num].sumd = befd[pos[l]];
s[num].sumt = beft[pos[r]];
return;
}
int mid = (l + r) >> 1;
build(num << 1 , l , mid);
build(num << 1 | 1 , mid + 1 , r);
s[num] = s[num << 1] + s[num << 1 | 1];
}
void update(int num , int l , int r , int x , int val)//更新点权
{
if(l > x || r < x)
{
return;
}
if(l == x && r == x)
{
s[num].sumt = val;
return;
}
int mid = (l + r) >> 1;
update(num << 1 , l , mid , x , val);
update(num << 1 | 1 , mid + 1 , r , x , val);
s[num] = s[num << 1] + s[num << 1 | 1];
}
void change(int x , int y , int t)//更改操作
{
if(dep[x] > dep[y])
{
swap(x , y);
}
update(1 , 1 , n , dfn[y] , t);
}
seg get(int num , int l , int r , int x , int y)//线段树上区间查找
{
if(l > y || r < x)
{
return null;
}
if(l >= x && r <= y)
{
return s[num];
}
int mid = (l + r) >> 1;
return get(num << 1 , l , mid , x , y) + get(num << 1 | 1 , mid + 1 , r , x , y);
}
int query(int x , int y)//查询操作
{
int res1 = 0 , nowt = 0 , res2 = 0 , nowd = 0 , totd = 0;
while(top[x] != top[y])
{
if(dep[top[x]] >= dep[top[y]])
{
seg awa = get(1 , 1 , n , dfn[top[x]] , dfn[x]);
totd = (totd + awa.sumd) % mod;
res1 = (res1 + (nowt * awa.sumd) % mod + awa.up) % mod;
nowt = (nowt + awa.sumt) % mod;
x = fa[top[x]];
}
else
{
seg awa = get(1 , 1 , n , dfn[top[y]] , dfn[y]);
totd = (totd + awa.sumd) % mod;
res2 = (res2 + (nowd * awa.sumt) % mod + awa.down) % mod;
nowd = (nowd + awa.sumd) % mod;
y = fa[top[y]];
}
}
if(x != y)
{
if(dep[x] >= dep[y])
{
seg awa = get(1 , 1 , n , dfn[y] + 1 , dfn[x]);
totd = (totd + awa.sumd) % mod;
res1 = (res1 + (nowt * awa.sumd) % mod + awa.up) % mod;
nowt = (nowt + awa.sumt) % mod;
}
else
{
seg awa = get(1 , 1 , n , dfn[x] + 1 , dfn[y]);
totd = (totd + awa.sumd) % mod;
res2 = (res2 + (nowd * awa.sumt) % mod + awa.down) % mod;
nowd = (nowd + awa.sumd) % mod;
}
}
res1 = (res1 + (nowt * nowd) % mod + res2) % mod;
return (res1 + (G * totd) % mod) % mod;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);
null.down = 0;
null.sumd = 0;
null.sumt = 0;
null.up = 0;//初始化
cin >> n >> G;
for(int i = 1 , a , b , D , T ; i < n ; i++)
{
cin >> a >> b;
edge e;
e.to = b;
cin >> e.D >> e.T;
g[a].push_back(e);
e.to = a;
g[b].push_back(e);
}
dfs1(1 , 0);
top[1] = 1;
dfs2(1 , 0);
build(1 , 1 , n);//预处理
cin >> Q;
int op , x , y , t;
while(Q--)
{
cin >> op >> x >> y;
if(op)
{
cout << query(y , x) << endl;//处理询问
}
else
{
cin >> t;
change(x , y , t);//处理更改
}
}
return 0;
}
附：谴责搬题人
充满了血泪的控诉，详情请看原帖。
题解：P9441 [ICPC2021 WF] Fair Division
· 阅读需 3 分钟
题目链接
解题思路
推导公式
设第 个人拿到的钱为 。
注意到 ，设 为 。
则 ，可得 。
所以 。
设 。
则 。
上下同乘以 并化简得到 。
证明互质
对于 的任何一个因数 ，可得 也是 的因数，而 与 互质，故 不是 的因数，所以 不是 的因数，但因为 是 的因数，所以 与 互质。证毕。
继续推导
因此，若要使 为整数， 必须能够整除 。
所以将 展开，得到 。
注意到 已经出现了两次，所以不做考虑，只需要验证 能否整除 即可。
因为 ，所以可以直接枚举 和 的值。
同时 需要不大于 ，数据范围实际上并不大，只需要用 __int128 确保在运算过程中不会超出范围即可。
参考代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
static const int INF = 2e18;
int n , m;
int mul(int a , int b)
{
return min(((__int128_t)a) * b , (__int128_t)INF);
}
int fpow(__int128 a , int b)
{
int res = 1;
while(b)
{
if(b & 1)
{
res = mul(res , a);
}
a = mul(a , a);
b >>= 1;
}
return res;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin >> n >> m;
for(int q = 2 ; fpow(q , n - 1) <= m && fpow(q , n - 1) != 2147483647 ; q++)
{
for(int r = 1 ; r < q ; r++)
{
int num = 0;
for(int i = 0 ; i < n ; i++)
{
num = min(num + mul(fpow(r , i) , fpow(q , n - i - 1)) , INF);
}
if(m % num == 0)
{
cout << q - r << " " << q << '\n';
return 0;
}
}
}
cout << "impossible" << '\n';
return 0;
}
题解：CF2033B Sakurako and Water
· 阅读需 1 分钟
题目链接
解题思路
因为只需要不小于零就可以了，所以想到每次可以选中完整的对角线。
于是代价就变成了每条从左上到右下的斜线上最小的值的绝对值（如果最小值是整数则为零）。
之后只要遍历每条斜线找出代价并累积就好了。
参考代码
#include <bits/stdc++.h>
#define N 505
using namespace std;
int T , n , a[N][N] , ans = 0;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin >> T;
while(T--)
{
ans = 0;
cin >> n;
for(int i = 1 ; i <= n ; i++)
{
for(int j = 1 ; j <= n ; j++)
{
cin >> a[i][j];
}
}
for(int i = 2 ; i <= n ; i++)
{
int minn = 0;
for(int j = 1 ; j <= i ; j++)
{
minn = min(minn , a[i - j][n - j + 1]);
}
ans -= minn;
}
for(int i = 0 ; i < n ; i++)
{
int minn = 0;
for(int j = 1 ; j <= n - i ; j++)
{
minn = min(minn , a[i + j][j]);
}
ans -= minn;
}
cout << ans << endl;
}
//system("pause");
return 0;
}
题解：CF2033C Sakurako's Field Trip
· 阅读需 2 分钟
题目链接
解题思路
因为可以随便转换，所以每对点的交换是对其他点对没有任何影响的。
所以考虑贪心，对于每个点对想办法减少代价。
设两个点分别为 （）,
故一定产生代价的情况可以分成以下四种：
-
且 或 （产生 的代价）
-
（产生 的代价）
-
且 或 （产生 的代价）
最后特判中间两个人会不会产生代价，这道题就这么做完了~
参考代码
#include <bits/stdc++.h>
#define N 200005
using namespace std;
int T , n , a[N];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin >> T;
while(T--)
{
cin >> n;
for(int i = 1 ; i <= n ; i++)
{
cin >> a[i];
}
int ans = 0;
for(int i = 1 ; i <= (n - 1) / 2 ; i++)
{//第二种情况会被前后各判一次，故不需要特判
if(a[i + 1] == a[n - i])
{
if(a[i] == a[i + 1] || a[n - i + 1] == a[i + 1])
{
ans++;
}
}
if(a[i] == a[n - i + 1])
{
if(a[i] == a[i + 1] || a[i] == a[n - i])
{
ans++;
}
}
}
if(n % 2 == 0 && a[n / 2] == a[n / 2 + 1])
{
ans++;
}
cout << ans << endl;
}
return 0;
}
题解：P10937 車的放置
· 阅读需 2 分钟
原题链接
解题思路
其实就是匈牙利板子
题意翻译一下就是每一行每一列都只能选一个点。
所以我们就可以建一张二分图，将行和列转化为点存储。
对于每一个可选的点，在行和列对应的点之间连一条边。
因为每行只能对应一列，所以能放的最大个数就是二分图的最大匹配。
参考代码
#include <bits/stdc++.h>
#define N 205
#define M 205
using namespace std;
int n , m , t , p[M] , ans = 0;
bool able[N][M] , vis[M];
vector <int> g[N];
bool match(int x)
{
for(int i = 1 ; i <= m ; i++)
{
if(able[x][i] && !vis[i])
{
vis[i] = 1;
if(!p[i] || match(p[i]))
{
p[i] = x;
return 1;
}
}
}
return 0;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
memset(able , true , sizeof able);
cin >> n >> m >> t;
for(int i = 1 , x , y ; i <= t ; i++)
{
cin >> x >> y;
able[x][y] = 0;
}
for(int i = 1 ; i <= n ; i++)
{
memset(vis , 0 , sizeof(vis));
if(match(i))
{
ans++;
}
}
cout << ans << endl;
return 0;
}