模拟赛题解/2025.9.23 模拟赛

T1-小 X 与宝藏（treasure）

题面

小 $X$ 游山涉水，想要找到埋藏在深林中的宝藏。

他偶然得到了这个深林的藏宝图，深林可以被看作一个 $n\times m$ 的矩阵。宝藏在地图中以 “$S$” 被标记出来，与此同时其他地方都是 “$.$”，同时宝藏的个数为 $t$，奇怪的是地图上并没有标明它描述区域的具体方位。

深林中有两条大河，一条是纵向的，一条是横向的。由于陆上的宝藏都已经被人他们开采完了，小 $X$ 只好转而寻求埋藏在两条大河深处的宝藏。可他并不知道大河具体在哪，也不知道大河的宽度有多少，地图上也没有标明。他唯一确定的，是两条大河横跨整个深林。

他通过小道消息得出两条大河中的宝藏的个数之和为 $k$。他想动用大批人马，对所有符合条件的地下进行搜寻。请你帮小 $X$ 统计大河位置情况的方案数。

如即是两条大河的合法位置，注意大河方向一个为横，一个为纵，且长度都是无穷大的，宽度至少为 $1$。蓝色和黄色分别表示了两条大河，注意它们相交的绿色区域被计算了两次贡献。

$1\leq n,t,k\leq 10^5,1\leq m\leq 100$。

题解

法一

发现两条河的宝藏数是可以分开计算的，于是对于原矩阵维护一个二维前缀和和后缀和，这样宝藏的数目就可以在两个点对上统计贡献，枚举其中一个点对，用数据结构寻找另一个点即可。

复杂度 $O(nm\log m)$。

法二

容易发现可以 $O(m^2)$ 枚举其中一条大河的宝藏数量。

直接 NTT 求对于不同行，某个宝藏数量的方案数，$O(t\log t)$。

因此时间复杂度为 $O(t\log t+m^2)$。

T2-小 X 与数字（number）

题面

小 $X$ 有 $n$ 个非负整数 $x_1,x_2,\cdots,x_n$，其中 $x_i<a_i$。 小 $X$ 很喜欢不一样的数字，但是不喜欢很大的数字，所以他希望 $x_i$ 的值两两不同，他认为满足这个限制的数列 $x$ 是好的。 给定 $a_1,a_2,\cdots,a_n$, 和 $L$, 你能帮他求出好的数列的个数 $\bmod998244353$ 的结果吗？

$n\leq 5000,a_i\leq 10^{15},L\leq 10^9$。

题解

考虑 $x_i\bmod L$ 取到 $k$ 的方案数，不难发现为 $\lfloor\frac{a_i}{L}\rfloor+[k<a_i\bmod L]$。先考虑 $L|a_i$，则此时任意一个排列的方案数都是 $\prod\frac{a_i}L$。

设 $b_i=a_i\bmod L$。考虑拆贡献，用乘法分配律展开，钦定 $i_1,i_2\cdots,i_t$ 选择了 $[k<b_i]$，那么为它们分配 $k$ 的方案数是 ，其中 $$ 是把所有 从小到大排序的第 个，而剩下的位置的方案数为 ，直接乘起来就是这种钦定的总方案数。

设 是按 的顺序排好的， 为考虑完前 个 ，钦定了 个的答案之和，这里的答案不算 的部分。那么 的转移为 。

最后答案为 。

$O(n^2)\text{dp}$ 即可。

T3-小 X 与序列（seq）

题面

给定一个 $n$ 个点的无根树，每个点有一个标号 $w_i$。

定义一条链 $(u,v)$ 的权值为按照从 $u$ 到 $v$ 的顺序把这条链的标号写下来之后，得到的序列的最长上升子序列长度。

你需要删掉一个点，使得剩下的链的权值的最大值最小。

$n\leq5\times10^5,1\leq w_i\leq5\times10^5$。

题解

先考虑怎么算出整棵树的 $\text{LIS}$。

求 $\text{LIS}$ 一般是用一个栈来维护每种长度的结尾最小最大是多少，在树上也同样可以这么做。并且栈的长度不超过深度，所以显然可以长链剖分优化。

然后注意到删点必然是删当前最长的一条链上的点，否则没有效果。

从链的两个端点分别跑一遍长剖，就可以算出删每个点的答案了。

T4-小 X 与停车（parking）

题面

小 $X$ 在一家饭店的停车场工作，她负责礼貌地接待重要的客人，保管他们的车钥匙并帮助他们停车。

一个晚上，她发现她管理的停车场中恰好有 $2n$ 辆车，它们共有 $n$ 种不同的颜色，每种颜色恰有两辆车。我们将颜色按 $1$ 到 $n$ 编号。

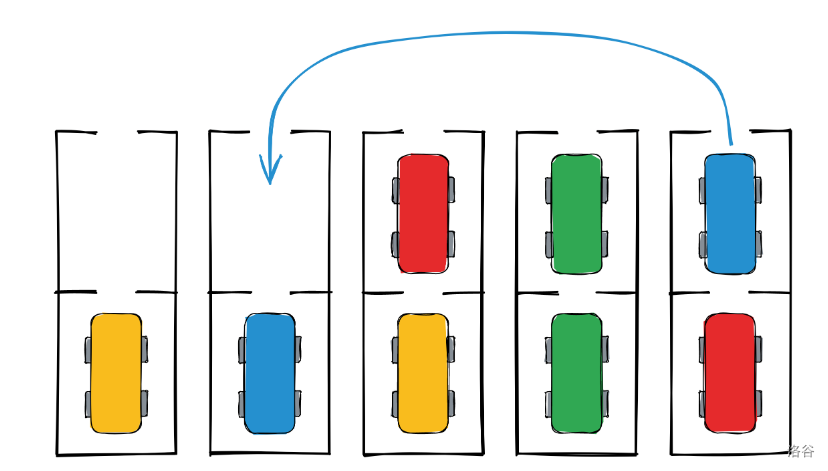
这张图描述的是一个样例，同时呈现了唯一的第一次驾驶。

停车场共有 $m$ 个车位，按 $1$ 到 $m$ 编号。每一个车位可以停下两辆车，一个车位只有一个入口，我们称靠近入口的为「顶上的车」，远离入口的为「底下的车」。一辆车可以从入口开出当且仅没有车挡着它。小 $X$ 在停车的时候，保证每个车位要么空，要么停满两辆。要么只有一辆底下的车。

小 $X$ 想要重新停放车使得每一对相同颜色的车都在一个车位里。我们并不关心车位对应什么颜色以及哪辆车在顶上哪辆车在底下。小 $X$ 将执行如下操作：

• 驾驶一辆可以驶出车位的车，将车开到另一个车位，满足：
  • 这个车位是空的，并把车停在底下的车位，或者，
  • 这个车位有且只有一辆与当前驾驶的车颜色相同的车。 小 $X$​ 想知道最少的操作次数与操作方案，请你解决这个问题。

如果操作次数正确，但方案构造错误，将得到 $20\%$ 的分数。

$1\leq n\leq m\leq2\times10^5$。

题解

若一个栈的栈底为 $x$，栈顶为 $y$，则称其为 $(x,y)$。

首先如果栈的两个颜色相同，则不会管它们了，不可能会把其中一个挪到一个空栈。每操作一次也最多匹配一个颜色。

假如其中一个栈 $s$ 满了，设其为 $(x,y)$，则 $x$ 要动的前提是把 $y$ 挪走了。我们用一个有向图刻画，对于这种情况我们连边 $y \to x$，这样每个点的出度和入度之和每时每刻都 $\leq 2$，这使得该图的形态很单一，可以尝试对每种形态逐一攻破。

在分析之前，我们要找出了一个颜色 $x$ 和其它颜色 $y$ 有连边说明有一对 $x,y$ 在同一个栈中。如果 $x$ 的两个度数不全说明有一个独占一个栈，即 $(x,0)$。

• 孤立点 （度数为 $0$）

设其为 $x$，则可以将 $(x,0),(x,0)$ 操作一次变为 $(0,x),(0,x)$。这样只用一步，不仅匹配了 $x$，还多了一个空栈。绝对是不亏的。

• 一条局部链（链上的点恰恰的点没有连边）

设其为 $a_1 \to a_2 \to \dots \to a_k$。

首先我们无法到孤立点x的贡献：只用一步，匹配一种颜色的同时，多出一个空栈。

我们发现 $a_1$ 的分布是 $(a_1,0)$ 和 $(a_2,a_1)$，则我们可以变成 $(a_1,a_1)$ 和 $(a_2,0)$，在匹配 $a_1$ 的同时去掉了 $a_1 \to a_2$ 这条边。我们可以一直这样做直到变成孤立点，这样在不借助其它栈的同时用 $k$ 步将栈删完，还多出一个空栈。

类似的，只要存在入度为 $0$，出度为 $1$ 的点，都可以通过这种方法一步一步匹配。我们可以用类似拓扑排序的方法将位于链上的点消除。

剩下入度为 $0$ 的点出度均为 $2$，所以我们有以下情况：

• $k$ 个点 $k$ 条边的环（即连通块中出度和入度均为1）。

• 一条非同向链，形如 $a_1 \leftarrow a_2 \leftarrow \dots \leftarrow a_k \to a_{k+1} \to \dots \to a_l \to \dots$，可以视为若干条有向链的两端点拼接得到，尾两端点均为链尾。

• 非同向链的两端点合并。

此时不同点都无法直接用一步匹配，只能在环或者非同向链上消除。移动的限制也说明了不能在两两端点之间消除，所以我们必须要先找到一连通块消耗掉的步数和额外的空栈，操作的实质已经不离散于之前的操作。此时我们必须要有至少一个空栈，否则没有合法方案。

• $k$ 个点 $k$ 条边的环

考虑合成，将环拆成两个栈为 $(a_2,a_1),(a_1,a_2)$，此时我们必须找到一个空栈 $(0,0)$，将这两个栈变为 $(a_1,0),(a_1,0),(a_2,0),(a_2,0)$。这样我们将环花一步操作拆开，并多了一个空栈。我们接着把 $a_1 \to a_2$ 这条边，设为 $a_1,a_2$，拆掉一个环，剩下的部分还是环。我们可以再这样继续拆，直至最后只剩一个栈，没法继续操作，已经是当前最优的方案，所以只要能优先清去，不会对其贡献的分产生影响。

• 一条非同向链}

此时我们要考虑从出度为2的点处断开，设其为 $x$，则形如 $y \leftarrow x \to z$，$y$ 和 $z$ 连出了两条链，此时 $x$ 所在栈为 $(y,x),(z,x)$，存在一个空栈 $(0,0)$。

此时，如果两端的链中有一条是有向链（这种链一定存在，就是最靠近链尾的两端的出度为2的点），设这时 $y$ 所在的链是向链。则可以用1步将 $(y,0),(z,x)$ 变为 $(y,0),(x,0)$，消除 $x \to y$ 的边。剩下的按照前述方法又会还原一个空栈，并且相同的时候链长度减小，效果和环不一样，甚至还在最后增加一个空栈。优先进行这种操作肯定不亏。

• 非同向链两端点合并

此时我们不妨不将两个出度为2的点 $x$，其为 $(y,x),(z,x)$，通过 $(0,0)$ 变为 $(y,0),(z,0),(x,x)$，这里要留1步才行，消去一个空栈，将剩下的安排为向同向链。这额外的1步和一个空栈不得不使用，但后续的清除时，所以它应放到最后处理。

只要模拟这样的过程即可，复杂度 $O(n)$。