学习笔记：扫描线

参考文献

一文读懂扫描线算法

前置知识

1. 线段树基础知识
2. 线段树染色问题基本概念
3. 离散化操作

引入

在洛谷 P5490 【模板】扫描线 & 矩形面积并中，我们需要求解在一个平面中的矩形面积并

其朴素暴力方法显然是用矩形面积和减去矩形面积交

因为矩形之间需要两两比较，因而复杂度为 $O(n)$，显然不足以通过本题

因此我们需要一个更高效的算法来解决有关问题

思路

分割

我们可以考虑将矩形面积并重新分割

如图中，可以将两个重叠的矩形分割成三个互不相交的矩形

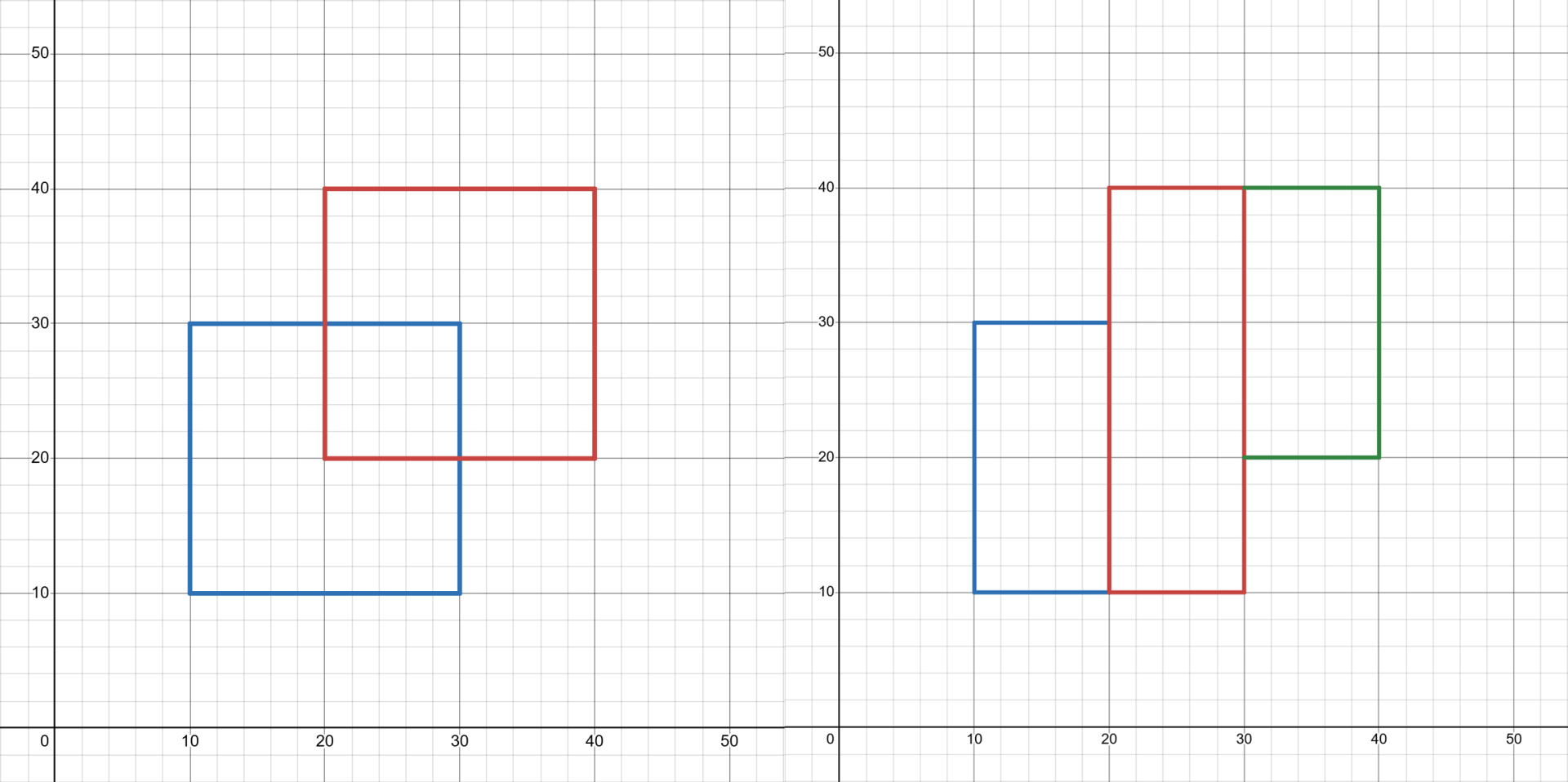
于是就可以将矩形面积并转化成右图中矩形的面积之和

计算方法也并不复杂， 只要从左往右扫，一个个加入即可（”扫描线“就这么来的）

计算

使用这种方法所需要的信息仅有两个：每个小矩形的宽度和高度

宽度：

将所有垂直于$x$ 轴的边挑出来，按横坐标从小到大排序，按位相减即可

高度：

鉴于每个小矩形的上下界可能属于不同的矩形，我们将垂直于 $x$ 轴的边进行分类

规定原矩形中横坐标较小的边为入边，较大的为出边

于是我们就可以逐条遍历，遇到入边时加，出边时减，维护每个区间内的矩形面积

以防区间过大，我们可以先将纵坐标离散化，缩小数据范围，使范围缩小到最多 $2n$ 个点

这样我们就可以建立一棵线段树来维护区间加减操作

*值得注意的是，这颗线段树的叶子节点应当是 $r=l+1$ 的，因为单点对统计块没有贡献

代码示例：

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

const ll N = 4000005;
ll cover[N] , le[N] , yy[N];

struct SL
{
    ll x , upy , downy;
    ll inout;
    SL() {}
    SL(ll x , ll y1 , ll y2 , ll io):x(x) , upy(y1) , downy(y2) , inout(io) {}
};
SL l[N];

bool cmp(SL &a , SL &b) {return a.x < b.x;}

void pushup(ll l , ll r , ll rt)
{
    if(cover[rt]) le[rt] = yy[r] - yy[l];
    else if(l + 1 == r) le[rt] = 0;
    else le[rt] = le[(rt << 1)] + le[(rt << 1 | 1)];
}

void update(ll yl , ll yr , ll io , ll l , ll r , ll rt)
{
    if(yl > r||yr < l) return;
    if(yl <= l&& yr >= r)
    {

        cover[rt] += io;
        pushup(l , r , rt);
        return;
    }
    if(l + 1 == r) return;
    ll m = (l + r) >> 1;
    if(yl <= m) update(yl , yr , io , l , m , (rt << 1));
    if(yr > m) update(yl , yr , io , m , r , (rt << 1 | 1));
    pushup(l , r , rt);

}

signed main()
{
    ll n , cnt = 0 , yr , yl , io;
    ll x1 , x2 , y1 , y2;
    cin >> n;
    for(ll i = 1 ; i <= n ; i++)
    {
        cin >> x1 >> y1 >> x2 >> y2;
        l[++cnt] = SL(x1 , y2 , y1 , 1);
        yy[cnt] = y1;
        l[++cnt] = SL(x2 , y2 , y1 ,  - 1);
        yy[cnt] = y2;
    }
    sort(yy + 1 , yy + cnt + 1);
    sort(l + 1 , l + cnt + 1 , cmp);
    ll len = unique(yy + 1 , yy + cnt + 1) - (yy + 1);
    memset(cover , 0 , sizeof(cover));
    memset(le , 0 , sizeof(le));
    ll ans = 0;
    for(ll i = 1 ; i <= cnt ; i++)
    {

        ans += le[1] * (l[i].x - l[i - 1].x);
        yl = lower_bound(yy + 1 , yy + len + 1 , l[i].downy) - yy;
        yr = lower_bound(yy + 1 , yy + len + 1 , l[i].upy) - yy;
        io = l[i].inout;
        update(yl , yr , io , 1 , len , 1);
    }
    cout << ans << '\n';
    return 0;
}